Tuyến liên kết – Khung cơ bản trong Cơ sở tạo hình
Tuyến liên kết – Khung cơ bản là dạng kết cấu nhiều thanh (tuyến liên kết) kết nối với hệ khung gốc (khung cơ bản) để tạo ra một diện phẳng, diện cong hay một không gian nào đó.
1. Tuyến liên kết – khung cơ bản trên mặt phẳng:
Trên mặt phẳng có hai đoạn thẳng AB và CD (gọi là khung cơ bản), trên đó đánh dấu các điểm tương ứng đều đặn nhau. Có các biến thể sau về sự liên kết hai khung cơ bản (AB; CD).
- Hai khung cơ bản song song với nhau, tuyến liên kết được đấu kết kiểu trực giao (hình 7.72a).
- Hai khung cơ bản song song, tuyến liên kết kiểu đảo chiều (hình 7.72b).
- Hai khung cơ bản không song song, lệch nhau. Các tuyến liên kết đấu nối tuần tự (hình 7.72c).
- Hai khung cơ bản không song song, các tuyến liên kết kiểu đảo chiều (hình 7.72d).
- Hai khung cơ bản nối liền nhau tạo thành đường gấp khúc. Tuyến liên kết đấu nối tuần tự (hình 7.72e).
- Hai khung cơ bản nối liền nhau tạo thành đường gấp khúc. Tuyến liên kết đấu nối kiểu đảo chiều (hình 7.72f).
- Khung cơ bản được kết thành đường cong đều. Tuyến liên kết đấu nối kiểu tuần tự và đảo chiều (hình 7.72g).
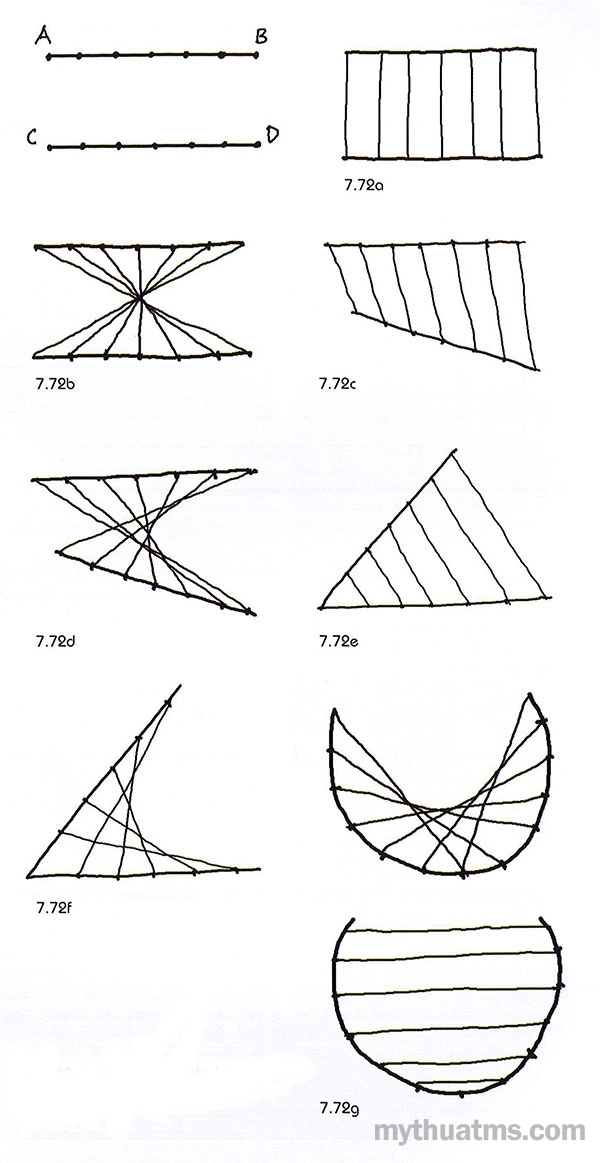
Hình 7.72: Biến thể tuyến liên kết khung cơ bản trên mặt phẳng
2. Tuyến liên kết – khung cơ bản trên không gian ba chiều:
Nếu lấy hình lập phương làm ô gốc không gian với các đỉnh là A, B, C, D, E, F, G, H thì hình này có 8 đoạn thẳng. Trên các đoạn sẽ đánh dấu các điểm với số lượng như nhau. Với hình hộp này sẽ có nhiều phương án chọn khung cơ bản và tổ chức các tuyến liên kết.
Ví dụ, đoạn thẳng AD và HG được chọn làm khung cơ bản, sẽ có hai phương án tạo tuyến liên kết như hình 7.73. Trong không gian ba chiều, khung cơ bản có thể là tuyến thẳng, tuyến cong, tuyến ba chiều hay một dạng hình học cụ thể nào đó. Hình vẽ 7.74 là ví dụ về tổ chức khung cơ bản – tuyến liên kết cơ sở hình gốc là khối lập phương.
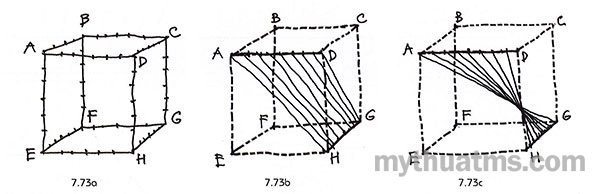
Hình 7.73: Hình lập phương và sơ đồ tuyến liên kết – khung cơ bản
a. Ô gốc lập phương có chia đoạn để hình thành tuyến liên kết trong không gian ba chiều.
b. Khung cơ bản là AD và HG, tuyến liên kết kiểu tuần tự.
c. Khung cơ bản là AD và HG, tuyến liên kết kiểu đảo chiều.
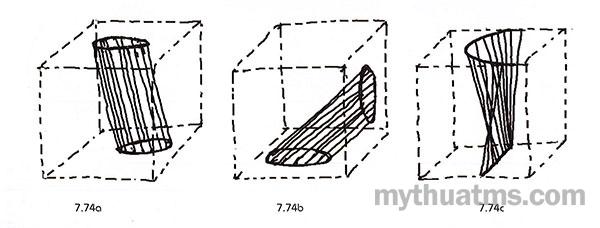
Hình 7.74: Các hình dạng khác nhau của khung cơ bản
a. Khung cơ bản có thể là hình tròn ở hai mặt phẳng song song đối nhau.
b. Khung cơ bản có thể là hình tròn ở hai mặt phẳng vuông góc nhau.
c. Tuyến liên kết có thể liên kết một khung cơ bản là đường cong tròn, một khung là đường thẳng.
3. Bài tập thực hành: Tuyến liên kết – Khung cơ bản
Tổ chức dưới dạng mô hình một cấu trúc tuyến liên kết – khung cơ bản. Xem ví dụ hình 7.75 (bài tập sinh viên).

Hình 7.75a: Cấu trúc này khung cơ bản gồm một tuyến cong và hai tuyến thẳng. Hợp nhóm tuyến liên kết
và khung cơ bản có vẻ tạo ra một không gian tương đối khép kín.

Hình 7.75b: Hai khung cơ bản có hình dạng tương đối tự do, cài giao thoa nhau tạo nên hệ khung chịu lực, cụt nhánh.
Các tuyến liên kết đan cài phức hợp.

Hình 7.75c: Một rãnh xoắn, hai khung lẻ phụ trợ làm nên khung cơ bản. Các tuyến liên kết đấu nối xoay tỏa trên rãnh xoắn.
Các tuyến phụ trợ tạo thêm vẻ đa dạng về hình cho tổ hợp.

Hình 7.75d: Một hợp nhóm khung và tuyến liên kết có tính chiều hướng rõ nhờ chuyển tiếp của các yếu tố thành phần qua dạng thức tuyến gấp khúc.

Hình 7.75e: Cấu trúc kiểu hướng tâm từ tám hướng thông qua tuyến và các bản diện chéo, phần trung tâm có sự biến động phi đối xứng tạo thêm vẻ đa dạng cho tổ hợp.

Hình 7.75f: Một bố cục đơn giản nhưng có hiệu quả thị giác thú vị, hai khung cơ bản xoay lệch nhau 90 độ, tuyến liên kết đấu nối chúng lại với nhau tạo nên bản diện cong hình rẻ quạt với nhiều khác nhau.

Hình 7.75g: Ở tổ hợp này có hai hệ tuyến liên kết bám bên trong khối kim tự tháp. Mỗi một hệ được trượt trên một cạnh cơ bản và đường chéo của đáy đã tạo nên hai mặt cong đối xứng nhau qua tâm đáy.

Hình 7.75h: Cấu trúc này có hai khung cơ bản đối nhau, một hình tròn, một hình đa giác. Tuyến liên kết đã tạo kiểu vặn xoắn cho khối nghịch lăng trụ.

Hình 7.75i: Một khung cơ bản là hình lập phương, các tuyến liên kết tổ chức đấu kết kiểu điểm với tuyến. Tổ chức cấu trúc kiểu giao thoa lặp lại và đối xứng.
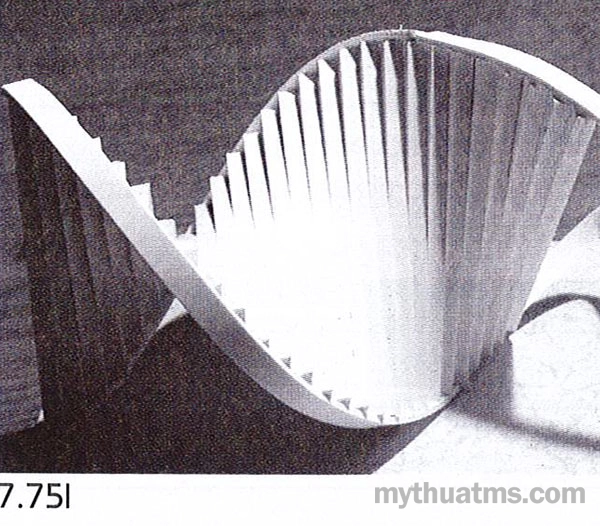
Hình 7.75l: Có hai khung cơ bản là đường xoắn lệch nhau. Các tuyến liên kết đấu nối hai khung tuần tự, song song và trực giao, một banmr diện cong vặn xoắn hình thành.

Hình 7.75k: Các khung cơ bản được đấu ghép với nhau kiểu cạnh tiếp xúc cạnh tạo ra chuỗi khung đa giác tương đồng. Các tuyến liên kế nội tại hợp nhóm kiểu tán xạ với tâm là điểm nối giữa hai khung cơ bản.

Hình 7.75m: Khung cơ bản hình lập phương được bổ sung thêm các cạnh chéo ở mặt cơ sở. Các tuyến liên kết đấu nối các cạnh chéo và cạnh cơ sở theo quy luật cân đối. Hợp nhóm được tạo ra tương đối phức tạp.

Hình 7.75n: Một khung cơ bản liền mạch kiểu xoắn ốc trụ, kết hợp tuyến liên kết tổ chức theo tuyến song song cách đều đã tạo nên các khe không gian kẹp giữa mỗi nhịp xoắn.

Hình 7.75p: Khung cơ bản hình lập phương được bao kín ba mặt. Ba mặt còn lại hở và khuyết một phần làm lộ ra hệ tuyến liên kế đấu nối theo ba cạnh thuộc ba diện khác nhau.
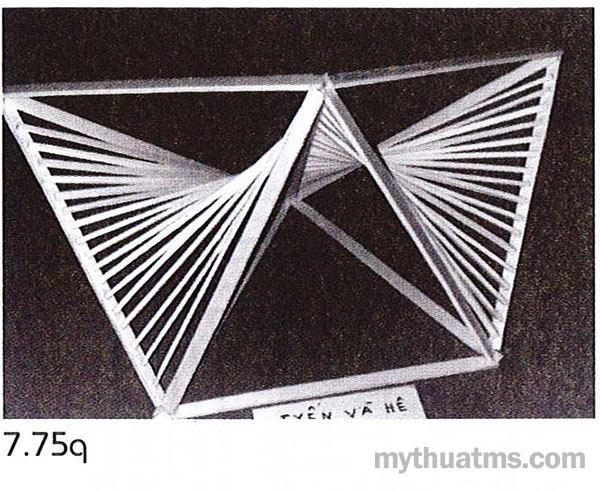
Hình 7.75q: Một khối đa diện nhiều mặt tam giác khung cơ bản. Hai hệ tuyến liên kết đối xứng tạo hai bản cong trong khối đa diện.

Hình 7.75r: Hai hệ tuyến liên kết – khung cơ bản độc lập được tổ hợp theo cách cài lồng vào nhau. Một dạng dẻ quạt một hình phễu.

Hình 7.75s: Một khung cơ bản hình kim tự tháp, diện đáy được chia làm bốn phần tạo nên bốn khung cơ bản các tuyến liên kế chuyển tiếp trong các khung này.

Hình 7.75t: Khối đa diện không đều làm khung cơ bản, bốn hệ tuyến liên kết tổ chức theo bốn kiểu khác nhau.

Hình 7.75u: Khối lập phương lớn chứa đựng khối lập phương nhỏ bên trong, hai khối không cùng chiều hướng. Một phần tuyến liên kết hai khối lập phương này.
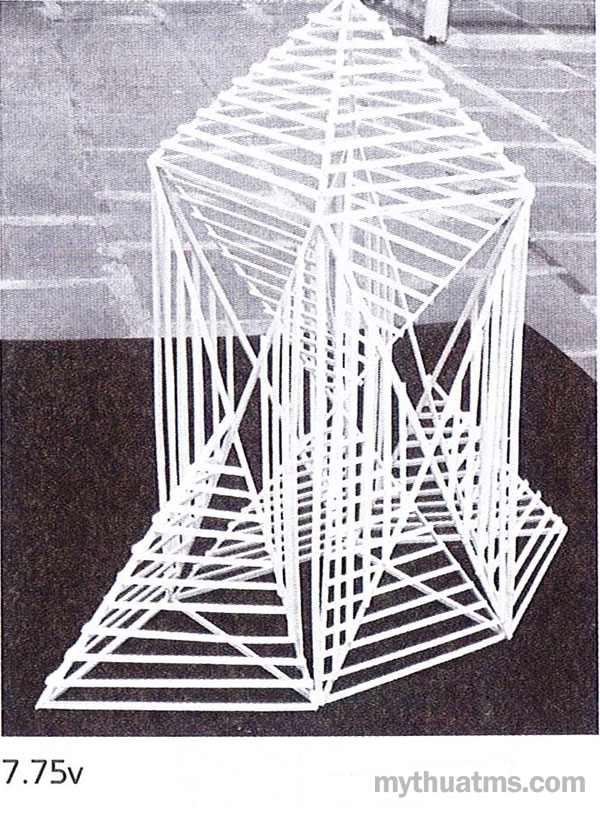
Hình 7.75v: Một khối nghịch lăng trụ được tạo thành từ phức hợp tuyến liên kết và khung cơ bản
>>> Nguyên tắc và tạo hình tượng Phật (Phần 1)
>>> Khung ngắm và sự liên quan đến bố cục