Các quy luật có liên quan đến tỷ lệ vàng
1. Quy luật chia ba:
Qua nghiên cứu tỷ lệ vàng với sự tương quan 1/1,618 hay 0,618/1 nhiều nhà nghiên cứu khác cũng muốn tìm ra con số tỷ lệ có giá trị tương đương với tỷ lệ tuyệt vời này và những người nghiên cứu sau này dã tư duy để tính theo hướng sau đây:
Nếu chúng ta nghiên cứu một con số bất kỳ chia cho 16 để tìm ra 1/16 và nhân cho 10 để có được con số mang tỷ sổ 16/10 hay 10/16 thì chúng ta có phân số tương đương 3/2 hay 2/3.
Vậy thì con số 3 này đã được một số nhà nghiên cứu khác về tỷ lệ tương quan tốt trong tranh ảnh trên một tổng diện tích bất kỳ để cho ra quy luật chia ba.
Qua tìm hiểu quy luật tỷ lệ vàng và quy luật chia ba chúng ta thấy có một số thuật ngữ gắn với hai quy luật này như sau:
* Nét mạnh: là những đường nét khoanh vùng “giới hạn” khu vực mà con mắt có thể nhìn bao quát và nhìn rõ hay giới hạn cho khu vực vàng.
* Điểm mạnh: là điểm hay chấm nằm ngay trên giao điểm của các nét mạnh.
* Khu vực vàng: là diện tích bị bao bọc, khoanh vùng bởi các nét mạnh, đây là khoảng không gian tốt để bố trí các nhóm hình thức quan trọng. Theo cách chia của quy luật tỷ lệ vàng và quy luật chia ba chúng ta cũng có khu vực vàng. Ở khu vực này chúng ta có thể bố trí các nhóm hình thù quan trọng.
* Điểm vàng: là giao điểm của các nét mạnh do cách chia 1/1,6 hay 0,6/1,0 theo quy luật tỷ lệ vàng. Tại điểm này chúng ta có thể bố trí các điểm nhấn từ chính đến phụ.
2. Quy luật số lẻ:
Trong nghệ thuật người ta thường đề cập đến thuật ngữ “sự đơn điệu” có nghĩa là trạng thái đều đều, tẻ nhạt, không sinh động. Đây là điều tối kỵ trong nghệ thuật. Ở đó cho thấy không có sự hiện diện của sự tương phản có biến hóa.
Để hình dung điều này, chúng ta thử suy nghĩ hay quan sát một người bước lên cầu thang nếu họ bước tuần tự 1, 2, 3, 4, 5, 6, 7, 8, 9…
Đây là bước liên tục và khoảng cách đều nhau về cao độ. Nếu ai đó lại bước 1, 3, 5, 7, 9, 11… Cũng là khoảng cách đều về cao độ (cách nhau 1 bậc). Cho dù ai đó có bước dài và sức khỏe mà lên thang theo các bậc: 2, 4, 6, 8, 10 (cách đều nhau 2 bậc). Như vậy mỗi sự thay đổi độ cao khi bước lên đều rất đều nhau!
Còn nữa, nếu chúng ta có 7 hay 10 ô màu mà đều tô một màu với sắc độ khác nhau và ô này cách đều nhau về độ đậm hay độ sáng, thế là chúng ta thấy dãy màu này tẻ nhạt, chán nhìn, không sinh động.
Về âm nhạc cũng vậy nếu âm này cách đều âm kia và cứ như thế tăng dần thì quả là buồn tai, buồn ngủ…
Tất cả những thí dụ trên đều cho thấy: khoảng cách đều = khoảng chẵn = sự đơn điệu. Bởi lẽ nó không có sự hiện diện của khoảng cách lẻ.
Trong lý thuyết bố cục nhiếp ảnh thì người ta nói rằng: “Trong lĩnh vực nhiếp ảnh thì những con số lẻ tốt hơn những con số chẵn”. Việc tạo thăng bằng do bố trí ở khu vực trung tâm chưa chắc hay bằng việc vận dụng tỷ lệ chênh lệch lẻ.
Sau khi chúng ta nhận xét những giả thuyết về việc đi lên cầu thang, chúng ta có thể kết luận rằng tất cả mọi giải pháp xử lý hình tượng, màu sắc, âm thanh mà dựa trên cơ sở sự chênh lệch chẵn đều dẫn đến sự buồn chán, đơn điệu, không hấp dẫn thị giác lẫn thính giác. Đó là điều chắc chắn bởi lẽ ở đó không có được sự chênh lệch lẻ.
Như vậy, khái niệm chẵn tức là có sự cách biệt đều nhau (khoảng cách, cao độ, diện tích, độ sáng, độ đậm, độ tươi…) chứ không phải con số chẵn: 2, 4, 6, 8, 10, 12, 14, 16 và khái niệm lẻ cũng không phải là: 1, 3, 5, 7, 9, 11, 13, 15…
Chính vì thế mà quy luật chênh lệch lẻ ra đời mục đích của nó là tạo nên sự sinh động. Thật ra đối với những nghệ sỹ kinh nghiệm thực hành sáng tác thì họ đều hiểu điều này từ khi có người cho nó là quy luật.
Vậy thì tỷ lệ chênh lệch lẻ là như thế nào? Chúng ta hãy quan sát các dãy số: 1, 2, 5, 7, 8, 9, 13, 15, 15,2 (15 phẩy 2), 17, 20, 20,8 (20 phẩy 8), 26… hay: 3, 3,5 (3 phẩy 5), 4,5 (4 phẩy 5), 6, 9,10, 10,8 (10 phẩy 8), 12, 13, 16, 17, 20, 21. Đấy là một thí dụ về khái niệm chênh lệch lẻ.
Chúng ta hình dung trên dòng nhạc có những nốt mà nhạc sỹ ghi thêm “dấu luyến” sang nốt kế tiếp. Điều này giống như tình huống chúng ta cố tý tô, làm cho màu này “nhòe” sang màu kia.
Chính những phần “luyến láy” (luyến lên, luyến xuống) hay “nhòe sang” làm cho hai nốt nhạc hay hai màu quyện vào nhau giống như sự lặp đi lặp lại có sự thay đổi chút ít… làm tăng thêm hiệu quả của các nốt trầm (màu đậm), những nốt cao (màu sáng hay tươi) là cơ sở tạo nên sự sinh động…
Trong xử lý màu sắc người ta có thuật ngữ chuyển dần màu này sang màu kia.
Trong âm nhạc có khi nốt sau cũng có cao độ ngang với nốt trước nhưng sau đó có khi lại diễn ra sự đột biến về cao độ ở các nốt kế tiếp…
Trong các bài hát có khi tông chủ đạo là “thứ” nhưng những bài hát có đến đoạn cuối thì chuyển sang “trưởng”. Đó cũng là cách tạo sự sinh động hay chuyển “tinh thần” của bài hát từ trạng thái buồn, sâu lắng lên cao trào. Thí dụ đoạn hát cuối của bài hát “Tiễn em” của cố nhạc sỹ Phạm Duy hay bài “Bâng khuâng chiều nội trú” của nhạc sỹ Nguyễn Trung Cang.
Trên thực tế, trong mỹ thuật (ngôn ngữ thị giác) hay âm nhạc (ngôn ngữ thính giác) thì vị trí chuyển đổi hay thời khắc biến hóa và mức độ thay đổi đều do sự chủ động của nghệ sỹ. Đây là yếu tố tạo nên sự chuyển động thị giác (thị giác, thính giác) có nhịp điệu, tiết tấu, sự sinh động.
Trong việc tính toán để tạo nên sự chênh lệch về diện tích, về sắc độ, về cường độ, về khoảng cách, chiều dài, chiều ngang, độ rõ hay mờ trong hình vẽ hay trong tranh cũng cần vận dụng quy luật lẻ.
Nói chung, tỷ lệ vàng, quy luật chia làm ba và quy luật lẻ là những kiến thức phục vụ cho việc bố cục tác phẩm mỹ thuật.
Tuy nhiên điểm đặc sắc của tác phẩm nghệ thuật thường nằm nơi cách nhìn, cách đặt vấn đề, giải quyết vấn đề, cái riêng, cá tính, thị hiếu thẩm mỹ, cảm xúc và tài năng diễn tả của chủ thể sáng tạo. Bởi lẽ, nếu ai cũng biết và vận dụng nhuần nhuyễn các quy luật mà lại thiếu những phần vừa nói thì tác phẩm sẽ khô cứng, không thu hút được mọi người.
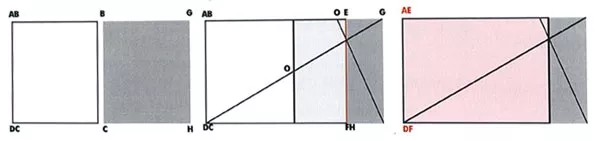
Cách tìm hình chữ nhật vàng theo kiến trúc sư Vitruvius
Đặt 2 hình vuông ABDC và BGCH liền cạnh nhau để có hình chữ nhật AGDH, kẻ đường chéo DG chia BC ra làm 2 đoạn bằng nhau (BO = OC). Kẻ đường chéo OH giao nhau với đường chéo DG. Dùng Eeke hạ một đường thẳng từ giao điểm này xuống cạnh đáy DH của hình chữ nhật và ta có đường thẳng thẳng đứng EF nối AG với DH. Kết quả chúng ta có một hình chữ nhật mới là AEDF – Đây là hình chữ nhật có tỷ lệ tương quan tốt nhất, được gọi là hình chữ nhật vàng.
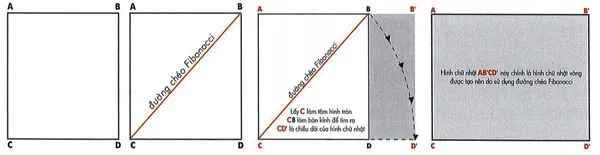
Cách tìm hình chữ nhật vàng
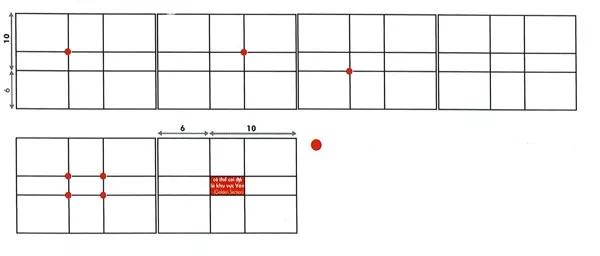
Tìm các điểm mạnh theo quy luật tỷ lệ vàng
Hình tròn màu cam: Vị trí các điểm mạnh: Nơi có thể bố trí các điểm nhấn chính hoặc phụ
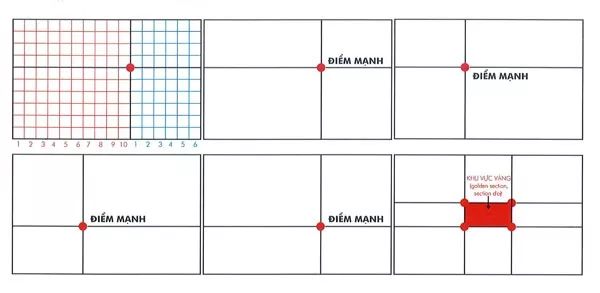
Tìm các điểm mạnh theo quy luật tỷ lệ vàng
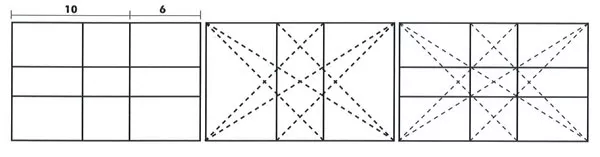
Cách chia bố cục theo tỷ lệ vàng
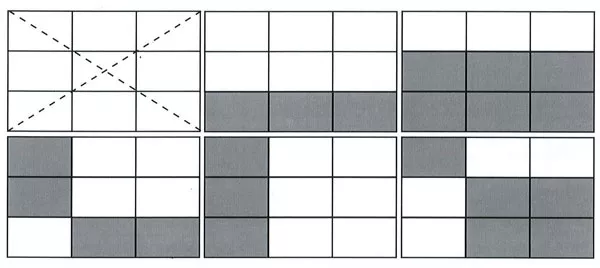
Cách chia bố cục theo quy luật chia ba
Chia bề ngang, bề dọc của diện tích bức tranh ra làm ba phần bằng nhau. Không bao giờ người ta bố cục điểm chính (điểm mạnh) ngay chính giữa bức tranh mà là bố trí nó ngay vị trí của 2/3 diện tích.
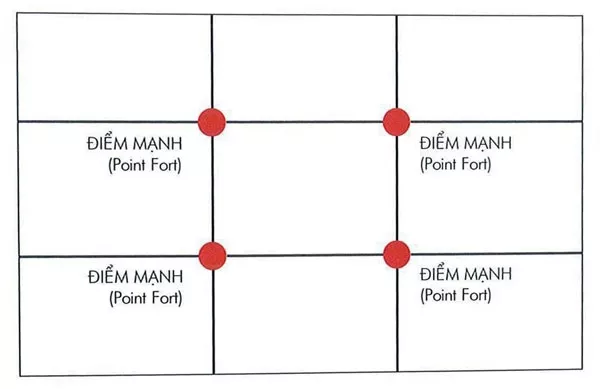
Vị trí điểm mạnh trong quy luật chia ba
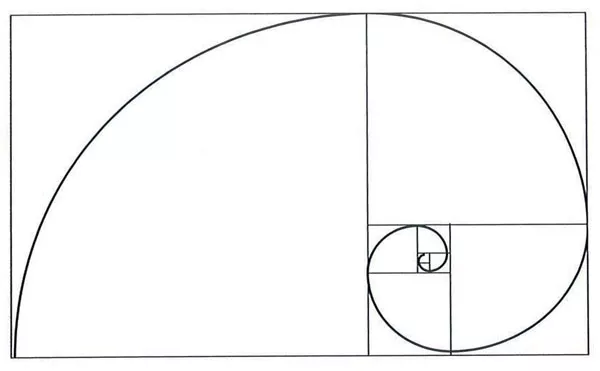
Hình xoắn ốc theo tỷ lệ vàng
- Bố cục theo quy luật chia ba:
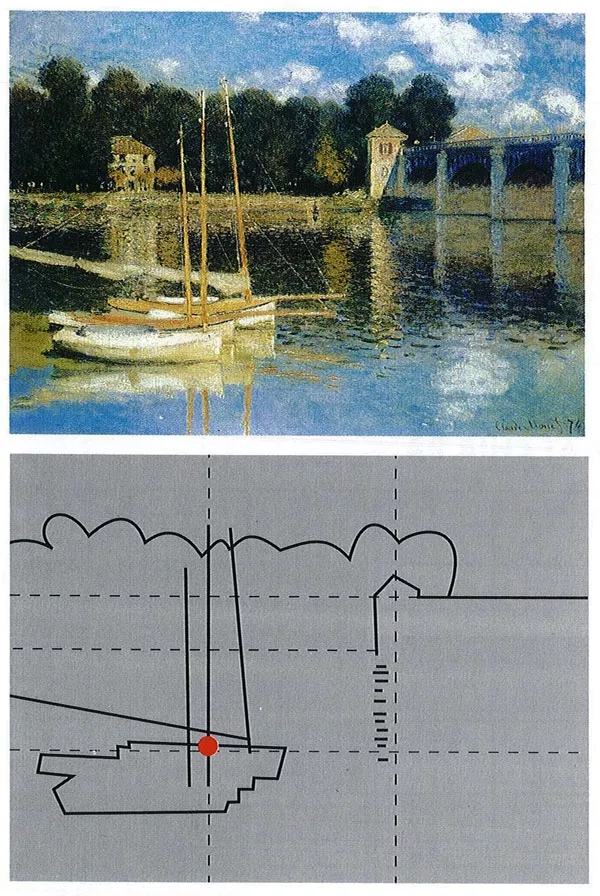
“Phong cảnh cầu Argenteuil” – Sơn dầu của họa sỹ Claude Monet
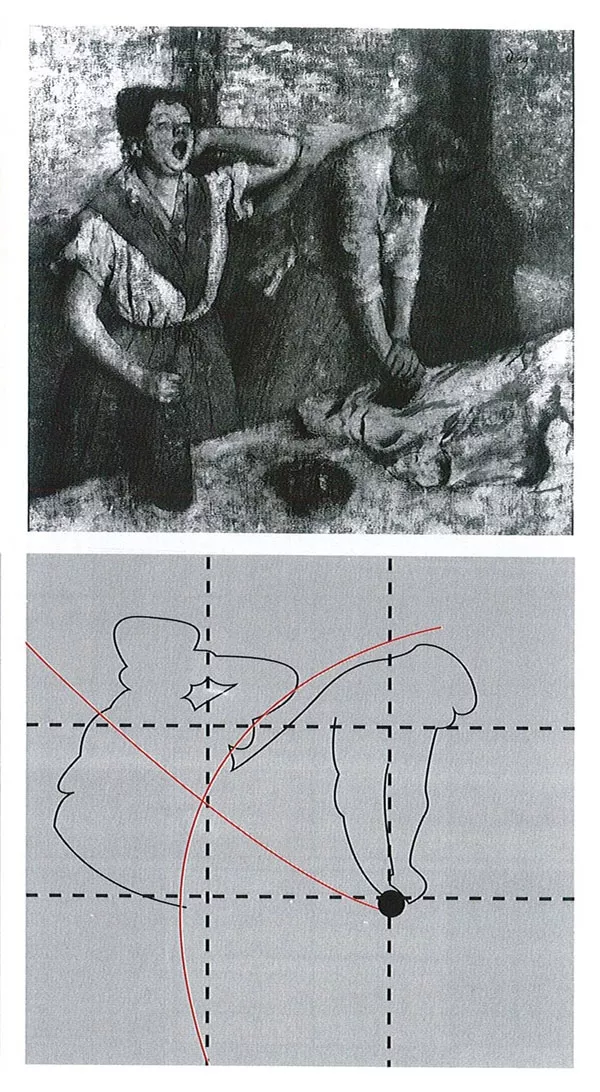
“Thợ giặt ủi” – Sơn dầu của họa sỹ E. Degas
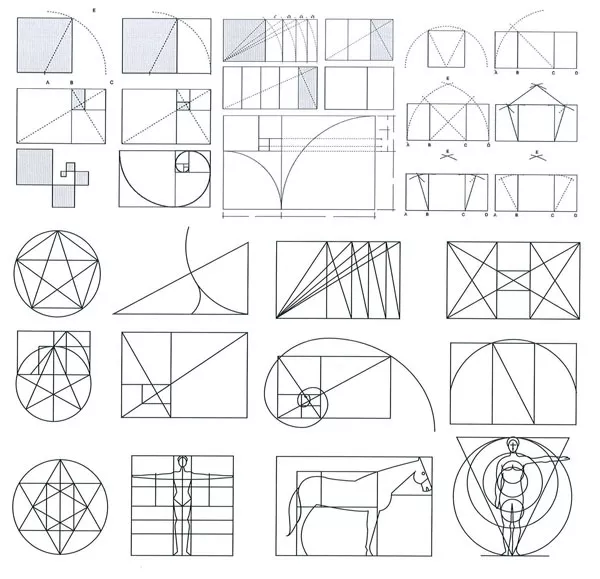
Minh họa về tỷ lệ vàng
- Bố cục ứng dụng theo tỷ lệ vàng:
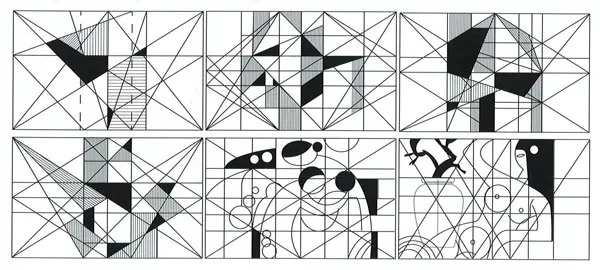

Vị trí điểm vàng hay điểm mạnh trong tranh – “Lòng tôn kính của các giáo sĩ” của họa sỹ Vélasquez

Phân tích bố cục bức tranh Guernica – Phác thảo và tranh thật của tác phẩm Guernica
(do họa sỹ Picasso sáng tác vào tháng 6 năm 1937). Bức ký họa để chuẩn bị cho tác phẩm Guernica

Sơ đồ bố cục của bức tranh
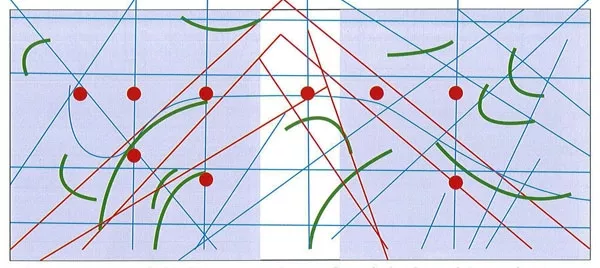
Ghi chú: Nét màu đỏ là những nét mạn. Các chấm đỏ là những điểm mạnh
Nét màu xanh lam là những nét mang tính chất tổ chức
Nét màu xanh lá cây thể hiện nhịp điệu, sự chuyển động

Biểu tượng về tỷ lệ vàng được thể hiện thành ngôn ngữ điêu khắc – “Pho tượng Vitruvian Man”
đặt tại quảng trường Belgrave, ở London – Anh Quốc
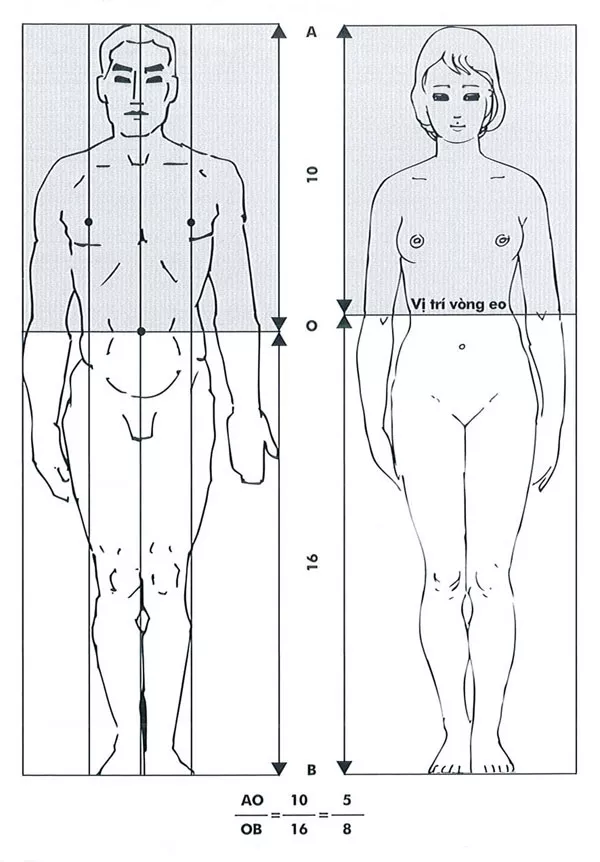
Tương quan tỷ lệ chiều cao cơ thể con người theo tỷ lệ vàng
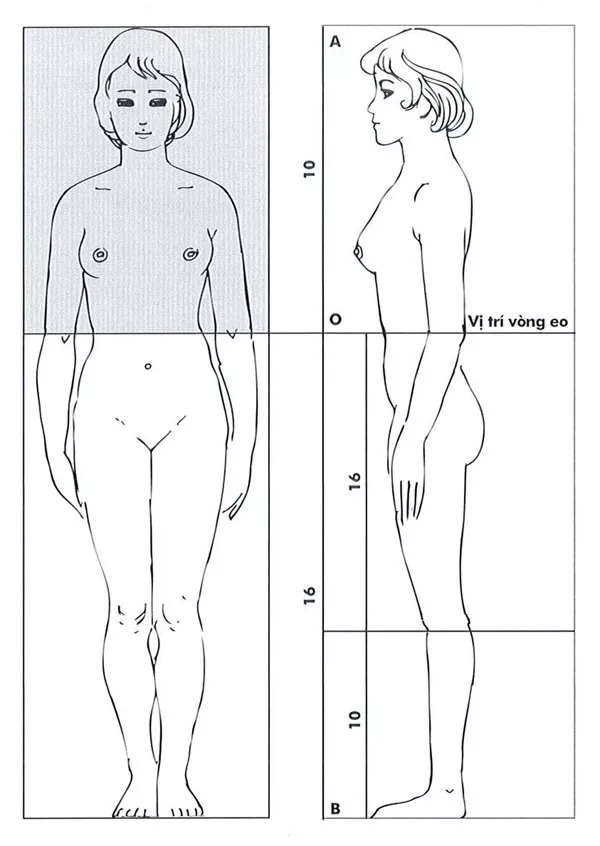
Tương quan tỷ lệ chiều cao toàn thân theo tỷ lệ vàng
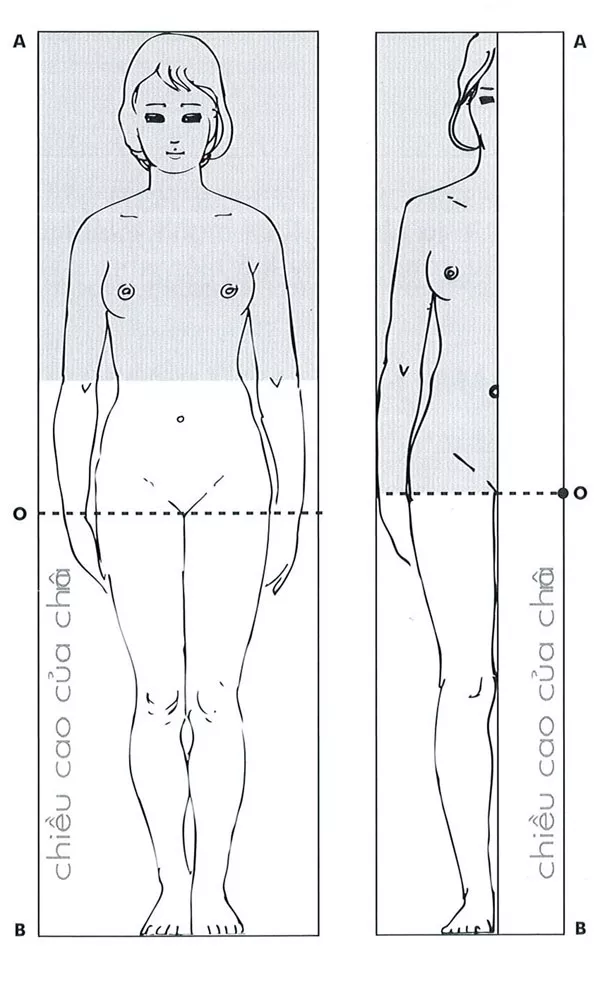
Cách phát triển tỷ lệ lý tưởng giữa thân và chiều cao của chân
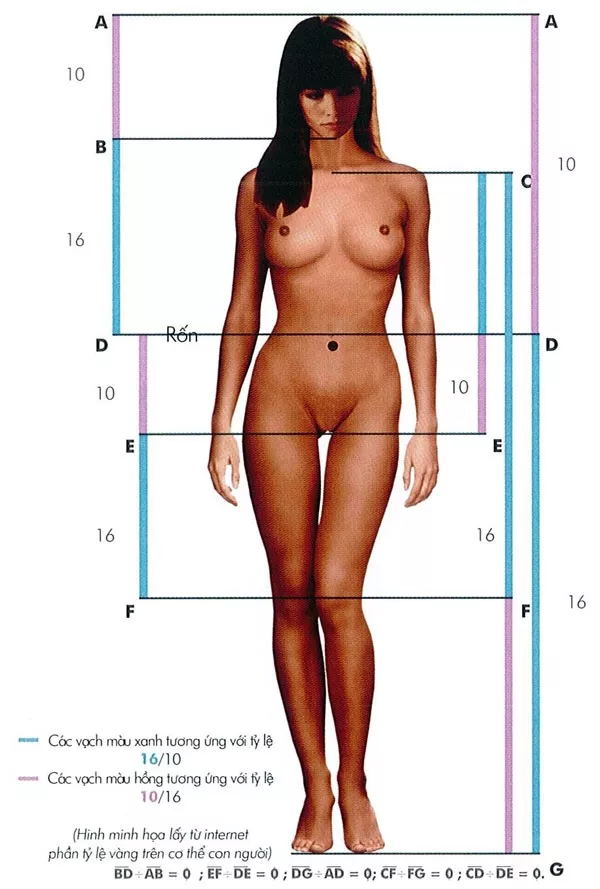
Tỷ lệ vàng trên cơ thể cân đối của nữ

Phân tích tác phẩm “La Gioconda” (Monalisa) của họa sỹ Léonard de Vinci
Họa sỹ, nhà bác học Léonard de Vinci (1452-1519) là thiên tài của thời đại Phục Hưng Ý về lĩnh vực hội họa thì tác phẩm “La Gioconda” được xem là một kiệt tác bởi nụ cười bí hiểm của nàng Monalisa. Tác phẩm này được coi là kinh điển của việc ứng dụng tỷ lệ vàng của nghệ sỹ này.
>>> Tỷ lệ cơ bản của cơ thể trong giải phẫu người
>>> Hình họa - Tỷ lệ người toàn thân