Nguyên tắc của sự đơn giản
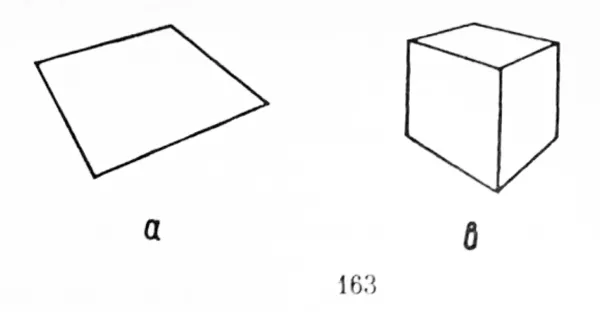
Các mô hình có dạng giống như được giới thiệu trong hình 163, có thể nhận được bằng cách chụp ảnh một hình vuông hay một khối lập phương qua một góc nghiêng. Trong phương án nổi khối, những mô hình này rất thường có hình dạng của các vật thể vật lý - những vật thể có hình chiếu chính là các mô hình đó. Hiện tượng này đã kích thích các nhà tâm lý học đúc kết ra một quy luật sau đây.
Bất chấp việc đang có những biến dạng xuất hiện trên võng mạc mắt, các đối tượng luôn được nhận thức hầu như tương ứng với hình dạng và kích thước vật lý của chúng (nguyên tắc bất biến). Mặc dù đối với các mục đích thực tiễn, định thức này nhìn chung là đúng, tuy nhiên nó đẩy chúng ta vào thế nhầm lẫn. Kết luận này đang dựa vào một tiêu chí ngẫu nhiên và, suy ra, không đưa ra khả năng hiểu được diễn biến của hiện tượng này.
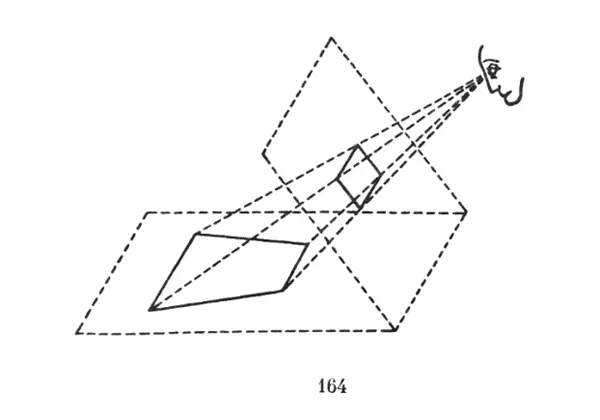
Giả sử rằng một hình thang được dựng bằng các đoạn thẳng nằm trên sàn nhà và phát sáng trong bóng tối, cách chủ thể nhận thức ở một khoảng cách nào đó. Hình thang này có tư thế sao cho nó hiển thị trong mắt người nhận thức như hình chiếu của một hình vuông (hình 164). Nếu người nhận thức nhìn vào hình thù này qua một ô ngắm, thì sẽ nhìn thấy một hình vuông nằm chính diện, bởi vì hình vuông là hình thù đơn giản nhất cho mô hình chiếu hình. Về mặt nhận dạng với đối tượng vật lý, nó nhìn có vẻ là một vật biến dạng, có nghĩa ở trường hợp này không có nguyên tắc bất biến. Chúng ta có thể đi tới một kết luận rằng, sự tương ứng giữa cái đang tồn tại trong không gian vật lý và cái đang được chúng ta nhận thức chỉ có trong trường hợp, khi hình dạng của đối tượng vật lý trong góc nhìn rút gọn là một hình thù tối giản, sao cho mô hình hình chiếu của nó được nhận thức là biến dạng. Thật may mắn, điều này xảy ra khá thường xuyên. Trong thế giới của những đồ gia công thì các hình chữ nhật, hình vuông, khối lập phương, các đường song song và các đường tròn được thấy rất phổ biến, ngoài ra, trong thiên nhiên còn đang có xu hướng tiến tới hình thức đơn giản. Nhưng khi hình dạng của các đối tượng là không chuẩn giản (như, chẳng hạn, các rặng núi), hình chiếu của chúng có thể không có vẻ là biến dạng của các hình thù đơn giản hơn. Suy ra, sự bất biến của hình dạng bị phá bỏ, và nhận thức nổi khối cần được dựa trên các yếu tố khác.
Quy luật, được mô phỏng trong hình 164, được ứng dụng cho các mục đích thực tiễn trong trang trí sân khấu và kiến trúc. Người ta thường mong muốn tạo ra một ấn tượng chiều sâu mạnh hơn những gì mà vật lý có thể làm.
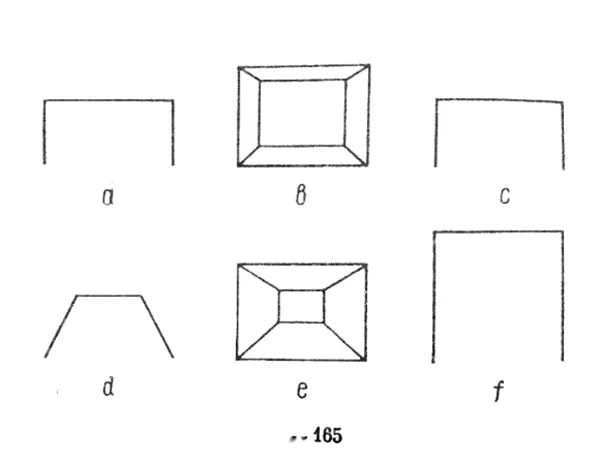
Nếu hoạ sỹ trang trí dựng trên sân khấu một căn phòng có hình dạng chuẩn giản với mặt sàn nằm ngang và các bức tường đứng vuông góc (hình 165а, nhìn từ phía trên), thị giả sẽ nhận thức được một mô hình hình chiếu 165b, và, suy ra, sẽ nhìn thấy một căn phòng gần giống như hình 165с. Tuy nhiên, nếu sàn nhà có góc nghiêng leo lên trên, còn trần nhà — chạy xuống dưới, thì các bức tường dạng hình thang sẽ hội tụ đâu đó ở điểm sâu của phối cảnh (hình 165d), độ dốc vật lý sẽ chồng chéo lên độ dốc chiếu hình, và trong kết quả sẽ được tạo ra một hình chiếu có dạng như hình 165е. Vì lỗ thủng nằm ở mặt tiền có các kích thước lớn, còn bức tường mặt sau lại nhỏ hơn nó, nên căn phòng dạng khối hộp sẽ được nhận thức là sâu hơn rất nhiều (hình 165f).

Một sơ đồ mặt cắt kiến trúc của cung điện Palazzo Spada. Nguồn: http://roma.andreapollett.com
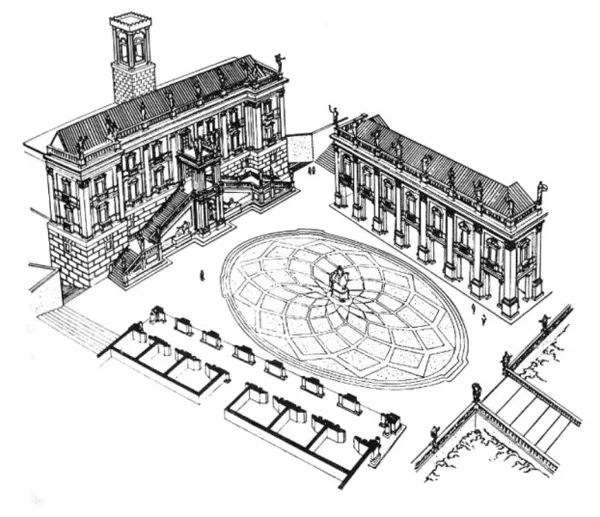
Tất cả điều đó đang nghịch lý với nguyên tắc bất biến, nhưng lại đồng thuận một cách chính xác với nguyên tắc của sự đơn giản. Để đưa ra như một ví dụ sáng sủa, có thể đề cập tới cung điện Palazzo Spada ở Rome. Vào khoảng năm 1635, khi Borromini xây lại cung điện này, ông đã dựng một mái vòm cột trụ thon dần về bên trong, để có được ấn tượng phối cảnh kiến trúc sâu thẳm. Nếu thị giả đứng trong khuôn viên và nhìn vào mái vòm, thì sẽ thấy một đường hầm dài với các cột đứng dọc theo hai cạnh bên hướng cái nhìn tiến sâu vào không gian mở, nơi có một bức tượng chiến binh dường như "khổng lồ". Nhưng, khi tiến sâu vào bên trong mái vòm, thị giả sẽ phải chịu đựng một thử thách với bệnh say sóng do bị mất định hướng không gian. Trong lệnh vụ của mình, Borromini chỉ có một khoảng đất hạn chế, và hàng cột đúng là bị ngắn. Nó được đo là gần tám mét rưỡi chiều dài tính từ cửa vòm phía trước đến cửạ vòm phía sau. Chiều cao của cửa vòm trước là năm mét tám, và chiều rộng là hơn ba mét một chút. Cửa vòm phía sau có chiều cao hai mét rưỡi, còn chiều rộng khoảng 90 phân. Trần vòm hơi dốc xuống dưới, sàn chếc nhẹ lên trên, các bức tường cạnh bên hội tụ, còn khoảng cách giữa các cột giảm dần. Khi tiến được tới pho tượng chiến binh, thị giả mới ngạc nhiên vỡ lẽ rằng nó hoàn toàn không to lớn theo kích thước. Các kiến trúc sư thời trung cổ đã đạt đến hiệu ứng tăng cường chiều sâu bằng cách ép các cạnh bên của các toà nhà thờ hội tụ tới chỗ mà dàn đồng ca hay đứng, và bằng cách rút giảm không gian bị chiếm bởi các cột.

St. Peter's Square and Basilica, 1909. Nguồn: wikipedia
Có cả các công trình sử dụng phương cách ngược lại. Các tác giả của chúng cố gắng bảo toàn hình dạng chuẩn giản trước ảnh hưởng biến dạng của phối cảnh và rút ngắn khoảng cách nhìn thấy. Xu hướng này được biểu hiện trong một hình đều góc xếp thành các hàng cột, được Bernini xây dựng trên quảng trường Thánh PhêRô ở Rô-ma, và quảng trường trước Campidoglio được Michelangelo thiết kế. Trong cả hai ví dụ đều có sự thon lại của phối cảnh hướng về phía thị giả đang tiến tới. Theo Vitruvius, độ dầy phần trên của cột trụ trong các ngôi đền Hy Lạp cổ tăng dần theo độ cao so với phần dưới. Giorgio Vasari vào thời Phục hưng đã khảng định: "...khi các bức tượng dành cho một vị trí cao, còn ở phía dưới không thể lùi đủ, để mà phán xét về chúng từ phía xa, và buộc phải đứng ngay phía dưới chúng, thì cần làm ra các hình thù đó sao cho chúng cao hơn một hoặc hai cái đầu". Nếu điều đó được làm, khi đó "các hình thù ở trên cao sẽ không bị giảm trừ khi đứng ở phía dưới và nhìn tới chúng từ dưới lên trên. Bởi vậy việc tăng cỡ áp đặt vào chúng sẽ được bù trừ bằng góc nhìn rút gọn, và theo tương tỷ này chúng đã có vẻ chuẩn mực và không bị béo lùn, đạt được sự ân sủng cần có"¹.
Quảng trường Thánh PhêRô được bao bọc từ hai bên bằng hai hành lang cột. Theo ngụ ý của Bernini, chúng tượng trưng cho vòng tay của nhà thờ đang ôm ấp thế giới. Các hành lang (colonnade) này được xây dựng vào năm 1660 và được hợp thành từ bốn dãy cột cao 20 mét và rộng 1.6 mét. Nguồn: lifeglobe.net
¹ Giorgio Vasari, Chuyện đời của các hoạ sỹ, nghệ sỹ điêu khắc và kiến trúc sư nổi tiếng nhất, «Nghệ thuật», M., 1956, t. I. p. 70.
Spaccato assonometrico di Piazza del Campidoglio. Nguồn: it.wikipedia
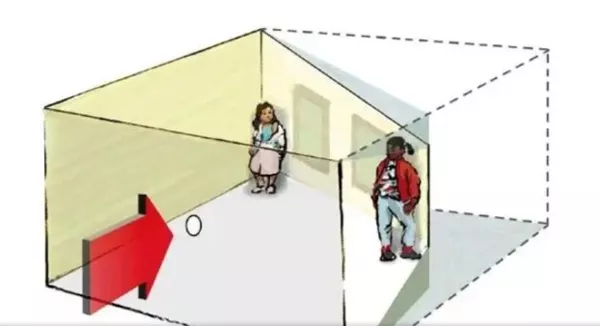
Hình minh họa: Conway Psychology
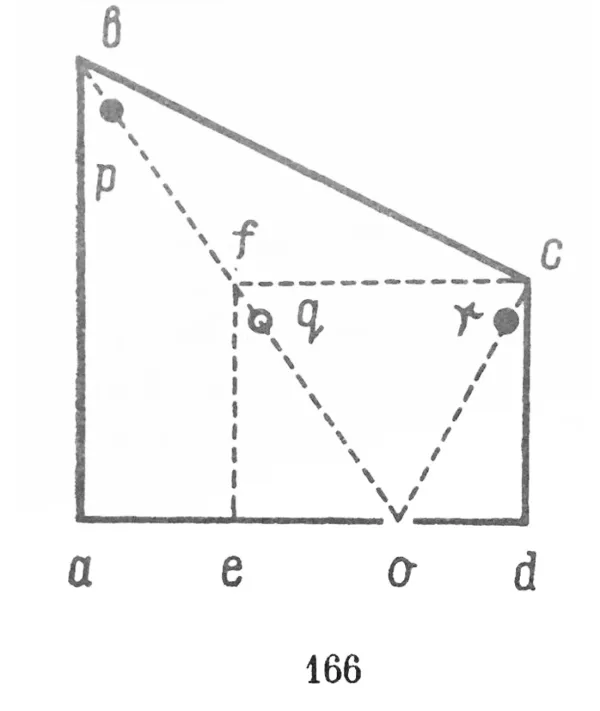
Mới đây, Adalbert Ames đã trình bày các yếu tố khác nhau giữa không gian vật lý và không gian tâm lý. Trong những thực nghiệm rất nổi tiếng này (hình 166) người chơi đã nhìn qua một lỗ ngắm nhỏ (o) vào một căn phòng mà anh ta cho là có dạng vuông vắn bình thường (efcd). Sơ đồ của căn phòng này — abcd. Căn phòng được thiết kế sao cho nó gọi trên võng mạc của chủ thể nhận thức một biểu trưng giống hệt như biểu trưng của một căn phòng có dạng vuông vắn. Với mục đích này, các bức tường, trần và sàn đã được tương ứng biến dạng và có một độ nghiêng lệch nào đó. Trong một căn phòng như thế sẽ xảy ra điều kỳ bí. Một người phụ nữ đứng ở điểm р sẽ được nhận thức như kiểu chị ta đang đứng ở điểm q, và, suy ra, nhìn có vẻ hoàn toàn là người lùn so với một người đang đứng ở điểm r. Người phụ nữ cao 180cm đứng ở điểm р nhìn có vẻ nhỏ hơn con gái của chị ta đang đứng ở điểm r. Ở bức tường phía sau có hai cửa sổ. Mặt của người phụ nữ nhìn ngang qua cửa sổ bên trái có vẻ nhỏ hơn nhiều so với mặt của cô con gái đứng ở cửa sổ bên phải.

Hiện tượng này sẽ còn là bí ẩn cho đến khi chúng ta nhớ lại được rằng, nhận thức của người đang nhìn qua lỗ ngắm bằng một mắt chủ yếu sẽ phụ thuộc vào mô hình hình chiếu đọng trên võng mạc của anh ta. Bất chấp việc mô hình này là nhận được từ một căn phòng biến dạng hay một căn phòng vuông vắn hoặc thậm chí từ ảnh chụp chúng, không có sự khác biệt nào, dù chỉ là một chút, không được quan sát thấy. Nếu căn phòng bị biến dạng được nhận thức là vuông vắn, thì để giải thích cho điều này đòi hỏi không nhiều lý lẽ hơn việc giải thích một dữ kiện, khi một căn phòng thực sự vuông vắn cũng được nhận thức là vuông vắn. Giải thích này, như tôi nghĩ, trong cả hai trường hợp sẽ là hoàn toàn như một. Mô hình hình chiếu là biến dạng của một hối hộp rỗng, và, suy ra, hình dạng đơn giản nhất có thể có được đang thâm nhập vào nhận thức không gian.
>>> Màu sắc có đo được không (Phần 1)