Các dạng hình thể trong không gian (Phần cuối)

4. Cấu trúc vách và ô không gian cơ sở:

* Hình lập phương và ô không gian cơ sở: Lấy một hình lập phương làm cơ sở. Bổ sung thêm hình lập phương theo chiều dọc, chiều ngang như vậy đã hình thành một hợp nhóm các hình lập phương sắp xếp đều đặn. Mỗi hình lập phương gọi là ô không gian cơ sở (hình 7.61). Ô không gian cơ sở có thể là tam giác, tứ giác, lục giác…

* Biến đổi hình bao ô không gian cơ sở: Hiệu quả ba chiều của tập hợp các ô không gian có thể thay đổi bằng cách điều chỉnh kích thước, hình dạng của mỗi ô không gian theo một số cách sau:

- Kéo dài theo một hướng của ô không gian cơ sở (hình 7.62a);

- Thay đổi kích thước ô không gian cơ sở theo một chiều kiểu vi biến (hình 7.62b);

- Các mặt ô không gian cơ sở có thể không vuông góc với mặt đáy (hình 7.62c);

- Các mặt bao quanh có thể được thay đổi thành các cạnh cong (hình 7.62d);

- Các vách bao ô không gian cơ sở có thể khuyết hoặc không có, chỉ tồn tại các yếu tố bên trong ô không gian cơ sở (hình 7.62e).

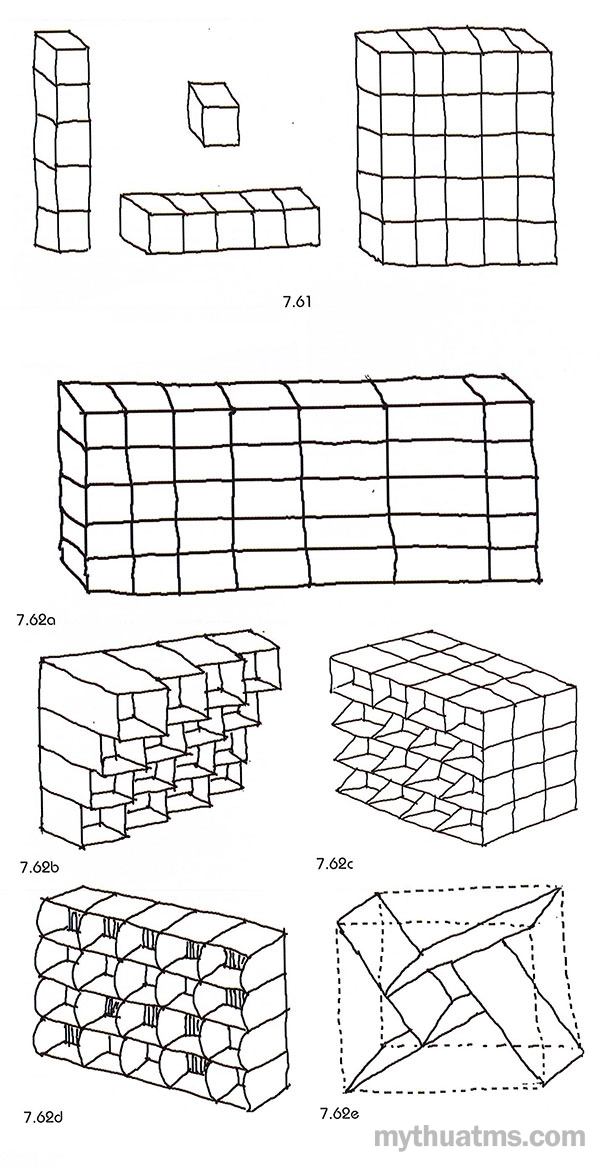
Hình 7.61: Hình lập phương là ô không gian cơ sở có cơ sở để tạo dựng hệ vách
Hình 7.62: Biến đổi hình bao ô không gian cơ sở

a. Kéo dài ô không gian cơ sở.

b. Thay đổi kích thước một chiều ô không gian cơ sở, tạo ra sự lồi lõm.

c. Các vách có thể nghiêng chéo.

d. Các mặt ngoài có thể thay đổi thành các cạnh cong.

e. Các vách bao ô không gian có cơ sở có thể không tồn tại.

*Biến đổi nội tại ô không gian cơ sở: Biến đổi nội tại ô không gian cơ sở tức làm thay đổi các thành phần đơn vị của ô không gian cơ sở.

Gọi các yếu tố tạo nên một ô không gian cơ sở là các thành phần đơn vị ô cơ sở. Các yếu tố này có thể là một diện, một tuyến. Sau đây là một số dạng biến đổi các thành phần đơn vị của ô cơ sở:

+ Thay đổi chiều hướng thành phần diện của đơn vị ô cơ sở (hình 7.63a).

+ Các diện thành phần đơn vị có thể là hình phẳng đầy (Positive) hoặc hình bị khấu trừ (Negative) (hình 7.63b).

+ Các diện thành phần đơn vị ô cơ sở được uốn, bóp méo, gấp, xé, khoét... (hình 7.63c).

+ Diện bao bên ngoài có thể cắt, khoét lôi ra ngoài đẩy vào trong, làm gáp nếp uốn cong... (hình 7.63d).

+ Các thành phần đơn vị có thể là dạng tuyến, mạng (hình 7.63e).

+ Các thành phần đơn vị ô cơ sở thay đổi theo cách biến đổi dần (vi biến) ở mỗi ô (hình 7.63f).

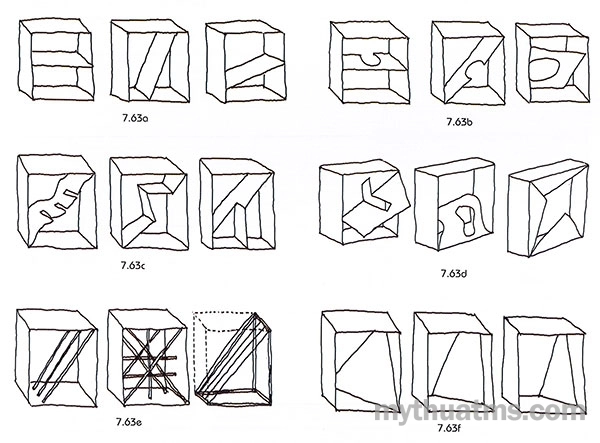
Hình 7.63: Biến đổi nội tại ô không gian cơ sở

a. Thay đổi chiều hướng diện ô cơ sở.

b. Các diện ô cơ sở có thể bị khấu trừ.

c. Các diện ô không gian cơ sở có thể được uốn, gấp nếp, chia cắt.

d. Các diện có thể được kéo ra đẩy vào rồi uốn cong, xẻ rãnh, gấp nếp…

e. Các thành phần ô không gian cơ sở có thể là dạng tuyến, dạng mạng.

f. Các thành phần của ô không gian cơ sở khi tập hợp có thể được thay đổi hình dạng dần dần.

BÀI THỰC HÀNH 7.4: Ô không gian cơ sở

Tạo một tổ hợp khối, không gian thông qua dùng ô không gian cơ sở. Dùng thủ pháp biến đổi đường bao, biến đổi nội tại ô không gian cơ sở. Xem ví dụ hình 7.64c.

Hình 7.64: Tạo khối, không gian thông qua dùng ô không gian cơ sở (bài tập sinh viên)

Hình 7.64a: Mỗi ô không gian cơ sở là một tứ diện đều trống một diện. Kết hợp kiểu diện tiếp xúc diện, trùng khít.

Hình 7.64b: Các ô không gian cơ sở là hình lập phương rỗng hai mặt, kết hợp kiểu cài lồng, chia làm hai lớp trước sau.

Hình 7.64c: Ba ô kiểu đa diện đều, khuyết diện kết hợp kiểu diện tiếp xúc diện, tổ hợp có dạng thức xoay tỏa.

Hình 7.64d: Các ô lăng trụ có kích thước diện đáy và độ dài biến đổi. Tổ hợp thống nhất về kết cấu, hình dáng lại biến đổi.

Hình 7.64e: Hợp nhóm các ô cơ sở hình lăng trụ ngũ giác. Mỗi ô lại được biến chuyển nội tại khác nhau, có ô hình sao, có ô khoét rỗng… Hợp nhóm các ô theo kiểu mạng, dạng tiếp xúc cạnh và đấu đỉnh.

Hình 7.64f: Các ô không gian hình trụ kết hợp kiểu diện tiếp xúc diện. Trong lòng mỗi ô được bổ sung hình lăng trụ, một dạng tổ chức khối trong khối, ô trong ô cơ sở.

Hình 7.64g: Các ô không gian cơ sở được xử lí cong ở diện bao ngoài. Diện nội tại đặt nghiêng, khấu trừ một phần và được bẻ ra ngoài.

Hình 7.64h: Diện đáy của các ô không gian cơ sở được khoét theo dạng mạng, phần nhánh có hình thức hữu cơ.

Hình 7.64l: Diện cong nội tại của mỗi ô không gian cơ sở là diện cong. Một phần diện cong của mỗi ô lại liên kết với nhau thành hình tròn khép kín. Thủ pháp liên kết này phá vỡ vẻ tuần tự của tổ chức mạng.

Hình 7.64k: Hợp nhóm ô không gian có cơ sở hình lập phương kiểu tiếp xúc diện và so le. Các diện đáy được khoét thủng, một phần được xoay, bên trong ô cơ sở có biến đổi đồng dạng.

Hình 7.64i: Biến đổi nội tại ô không gian cơ sở theo hai cách tạo diện chéo và hình vuông xoay tỏa. Tổ hợp đã tạo được vẻ đa dạng trên nền của ô vuông.

Hình 7.64m: Các ô không gian cơ sở kết hợp với nhau theo nhiều cách, tiếp xúc đỉnh, tiếp xúc cạnh, xoay để thay đổi chiều hướng. Các thành phần nội tại có hình dáng cơ bản giống nhau nhưng do thay đổi chiều hướng mỗi ô cơ sở nên đã tạo được tổ hợp biến đổi sinh động.

Hình 7.64n: Hai dạng loại ô không gian cơ sở. Một tạo diện nghiêng và một tạo ô nội tiếp bên trong kết cấu kiểu diện tiếp xúc diện.

Hình 7.64o: Các ô không gian cơ sở kết hợp kiểu tiếp xúc diện chiều hướng thay đổi. Các thành phần trong ô có hình dạng tương tự nhau.

Hình 7.64p: Một kiểu ô không gian lập phương kết hợp tiếp xúc diện và thay đổi chiều hướng ở một số ô được chia nhỏ đồng dạng bên trong.

Hình 7.64r: Các ô kết hợp tiếp xúc, giật cấp. Diện bên trong được đặt hơi nghiêng và có sắc độ đậm nhạt. Mỗi ô là đơn giản nhưng tổ hợp lại tạo được vẻ đa dạng, phong phú về sắc độ và hình.

Hình 7.64q: Các ô cơ sở hình trụ kiểu cánh lá, kết hợp theo kiểu cận kề, tiếp xúc bờ bao cơ sở mật độ mau thưa được thay đổi ở từng khu vực.

Hình 7.64s: Ô không gian cơ sở lăng trụ tam giác, kết hợp kiểu cạnh tiếp xúc cạnh và giật cấp.

5. Các lớp diện tạo khối: Việc hiểu cách tạo ra khối và biến đổi khối thông qua thủ pháp biến hình như: co, kéo, cắt, khấu trừ, vặn xoắn là quan trọng đối với các kiến trúc sư và các nhà thiết kế.

* Biến đổi khối thông qua biến đổi các lớp diện: Chúng ta biết rằng một mặt, một diện có thể được thể hiện bằng một loạt các tuyến (hình 7.65a). Một khối có thể được mô tả bằng một sêri các mặt, các lát cắt ngang khối (hình 7.65b).

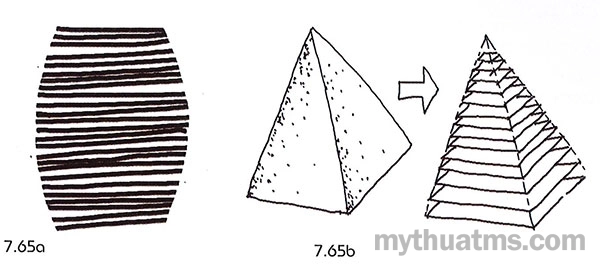
Hình 7.65:

a. Tập hợp tuyến tạo nên diện.

b. Tập hợp diện tạo nên khối.

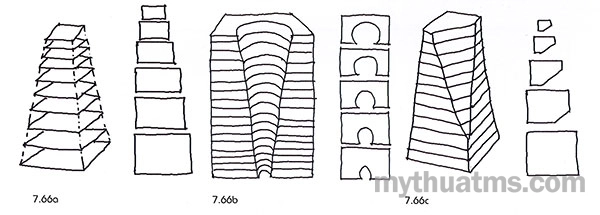
Hình 7.66a: Lặp lại về hình dạng, vi biến về kích cỡ.

Hình 7.66b: Biến đổi khối bằng cách vi biến hình dạng, lặp lại kích cỡ.

Hình 7.66c: Thay đổi dần cả về kích cỡ và hình dạng.

Bởi vậy, để dựng lên một hình khối, có thể tập hợp một loạt lát cắt. Khi các lát cắt có sự thay đổi về hình dạng, hình khối cũng sẽ thay đổi theo.

Sự vi biến, sự biến đổi dần của các lát cắt sẽ tạo ra sự chuyển dạng cho khối. Sau đây là các dạng biến đổi cơ bản:

a. Vi biến về kích cỡ lặp lại về hình (hình 7.66a).

b. Vi biến về hình, lặp lại về kích cỡ (hình 7.66b).

c. Vi biến cả hình và kích cỡ (hình 7.66c).

d. Biến đổi chiều hướng.

Chiều hướng các lát cắt có thể được biến đổi theo ba cách (hình 7.67):

- Xoay quanh trục thẳng đứng (a);

- Xoay quanh trục nằm ngang (b);

- Xoay quanh mặt phẳng của chính nó (c).

Quay quanh một trục thẳng đứng các lát cắt khi đó sẽ thay đổi về vị trí và không song song với nhau. Hình 7.68 cho thấy các lát cắt được sắp xếp tạo nên một vành tròn hướng tâm hoặc hình lượn sóng, gấp khúc.

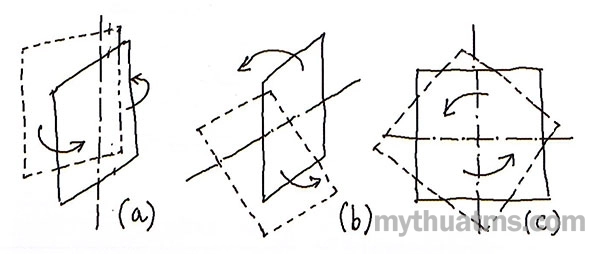
Hình 7.67: Tạo khối, không gian thông qua dùng ô không gian cơ sở

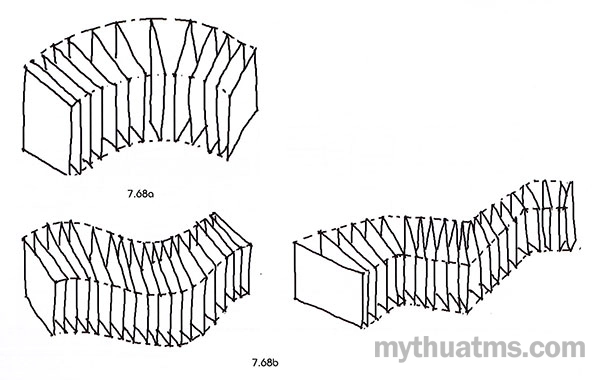
Hình 7.68: Các diện xoay quanh trụ đứng

a. Các diện tạo nên vành tròn.

b. Các diện tạo nên đường lượn sóng và gấp khúc.

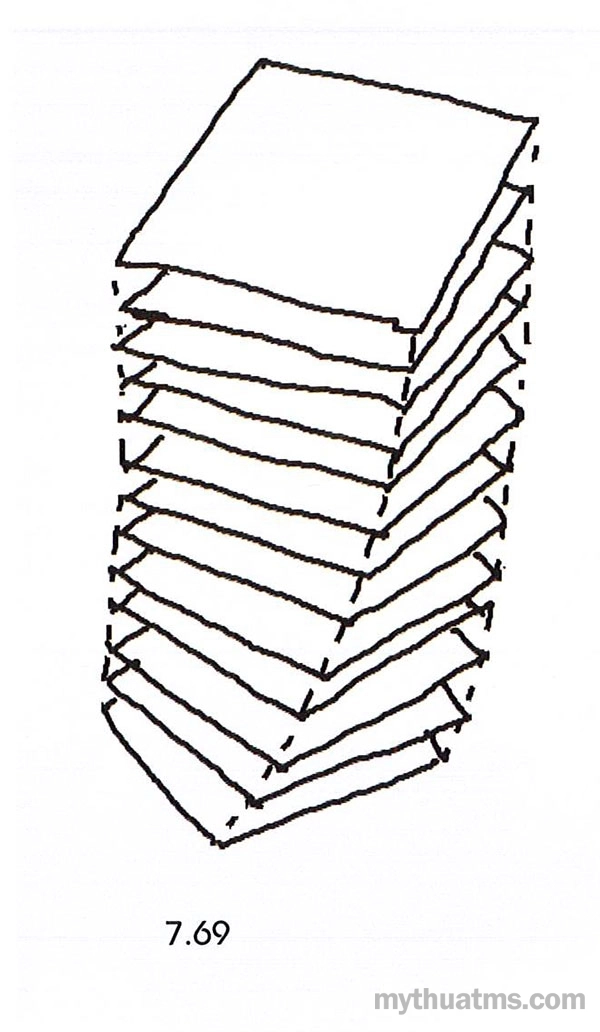
Hình 7.69

Xoay trong mặt phẳng của bản thân diện, khi đó các góc và cạnh của lát cắt thay đổi về vị trí nhưng phương ngang của lát cắt không thay đổi. Việc quay như vậy cho kết quả một hình vặn vỏ đỗ. Đây là một dạng của cấu trúc xoay tỏa. Xem hình 7.69.

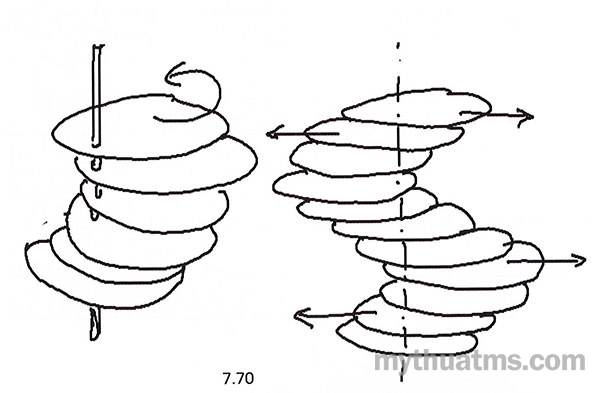
Hình 7.70: Xoay trượt các diện

Các lát cắt có thể song song, không thay đổi hoặc thay đổi hình dạng dần dần nhưng xoay tỏa đều đặn quanh một trục thẳng đứng vuông góc với các lát cắt (hình 7.70), hay trượt ngang (tịnh tiến), hoặc là vừa xoay vừa trượt.

Các diện có thể thay đổi hay không thay đổi hình dạng nhưng được xoay quanh một trục (tức đổi chiều hướng), trượt ngang (không thay đổi chiều hướng), hoặc vừa xoay vừa trượt.

BÀI THỰC HÀNH 7.5: Các lớp diện tạo khối

Dùng cách biến đổi dần kích thước, hình dạng; thay đổi chiều hướng, xoay, trượt… các diện để tạo nên khối hình.

Xem ví dụ hình 7.71.

Hình 7.71: Một sê-ri diện tạo

Hình 7.71a: Lặp lại y nguyên hình dạng một bản diện cong hình cánh lá. Các bản diện này xoay quanh trục thẳng đứng. Hợp nhóm mang dáng vẻ cong mềm mại.

Hình 7.71b: Trong trường hợp này cũng là sự lặp lại y nguyên hình vuông khuyết cạnh. Các hình vuông được quay quanh chính mặt phẳng của nó với góc quay đều đặt, lấy tâm hình vuông làm trục. Hình khối chung có dạng vặn, xoắn, các khe rãnh cong xuổi dài.

Hình 7.71c: Với hình tròn khuyết và lặp lại y nguyên về hình dạng nhưng xoay quanh trục trung tâm tổ hợp diện đã tạo nên một khối hình trụ có khe rãnh chạy cong xoắn luồn bên trong.

Hình 7.71d: Một khối lăng trụ cạnh xoắn được hình thành từ sự sắp xếp các diện ngũ giác. Điều đặc biệt ở đây là diện ngũ giác quay quanh (xoay quanh) trục trung tâm và độ dài mỗi cạnh thay đổi dần. Việc thay đổi này đã tạo cho khối chỗ mỏng, chỗ dầy, bề rộng diện đứng của khối lăng trụ luôn thay đổi.

Hình 7.71e: Một khối tháp không đều, được tham tạo bởi các diện đa giác theo cách biến đổi dần hình dạng và kích cỡ. Các đa giác vuông, hình thang, chữ nhật biến đổi uyển chuyển đã tạo các kiểu vát cạnh khác nhau cho khối.

Hình 7.71f: Việc bố trí 16 diện cong dạng hữu cơ lặp lại về hình dạng theo cách xoay quanh trục ngang đã tạo ra tổng thể khối dáng vẻ mềm mại và có vẻ phức tạp về hình.

Hình 7.71g: Một khối hình quả trứng khuyết được tạo từ cách sắp đặt một phần hình tròn cùng chiều hướng nhưng thay đổi dần về kích cỡ và hình dạng.

Hình 7.71h: Các hình tròn khuyết với các phần khuyết bằng nhau nhưng đường bao lớn dần của hình tròn cộng thêm việc xoay dần quanh trục trung tâm để tạo nên khối trụ không đều có phần khấu trừ mềm mại.

Hình 7.71i: Hợp nhóm một phức hợp các đa giác, các đa giác ở phần dưới không xoay nhiều và có hình đơn giản, càng lên trên càng thấy rõ sự cài lồng hai loại đa giác, một xoay ít và một xoay nhiều. Việc cài lồng này mang lại vẻ khác biệt giữa trên và dưới.

Hình 7.71k: Xoay tỏa 30 đa giác nhiều cạnh gấp khúc và biến đổi dần.

Hình 7.71l: Một khối với mỗi phần của khối rất khác nhau và có vẻ kì dị. Đây là kết quả của sự lặp lại và biến đổi dần ba loại hình dạng, diện được thay đổi nhanh từ dưới lên trên.

Hình 7.71m: Các hình dạng lá sen được biến đổi theo cách trượt ngang, xoay quanh tâm tạo nên khối trụ khuyết mềm mại.

Hình 7.71n: Một khối lăng trụ nằm ngang. Các hình vuông là bán diện cơ sở, lỗ tròn đục trên diện này di chuyển dần dần, tạo nên rãnh xoắn.

Hình 7.71q: Sự sắp xếp một loạt hình bỏ cạnh có dạng thẳng biến đổi dẫu về kích cỡ, hình dạng và xoay tạo ra khối hình tầng bậc, góc cạnh.

Hình 7.71p: Nhìn thoáng qua hình khối này có vẻ được tạo ra bởi phức hợp nhiều loại diện, nhưng thực chất chỉ là cách xoay một hình tròn khuyết quanh trục trung tâm.

Hình 7.71t: Một hình vuông biến đổi to dần rồi thành hình chữ nhật. Các phần khấu trừ diện thay đổi dần. Hợp nhóm các diện theo kiểu trượt đã tạo nên khối lăng trụ cong mềm.

Hình 7. 7r: Hình vuông khoét đồng dạng ở giữa được xoay đều tạo ra các rãnh xoắn ở bờ cạnh.

Hình 7.71s: Cũng hình vuông này xoay, cắt bỏ bờ cạnh. Hình chụp trong lòng khối có dạng vặn xoắn, các mặt phẳng cong, ngả đều.

Hình 7.71u: Hai hình viên phân bằng nhau và 1 hình vuông kẹp giữa biến đổi theo cách xoay dần quanh trục trung tâm, các hình này kích cỡ, hình dạng không đổi nhưng vẫn tạo được khối hình phức hợp uyển chuyển.

6. Tuyến liên kết – Khung cơ bản: Tuyến liên kết - khung cơ bản là dạng kết cấu nhiều thanh (tuyến liên kết) kết nối với hệ khung gốc (khung cơ bản) để tạo ra một diện phẳng, diện cong hay một không gian nào đó.

* Tuyến liên kết - khung cơ bản trên mặt phẳng: Trên mặt phẳng có hai đoạn thẳng AB và CD (gọi là khung cơ bản), trên đó đánh dấu các điểm tương ứng đều đặn nhau. Có các biến thể sau về sự liên kết hai khung cơ bản (AB;CD).

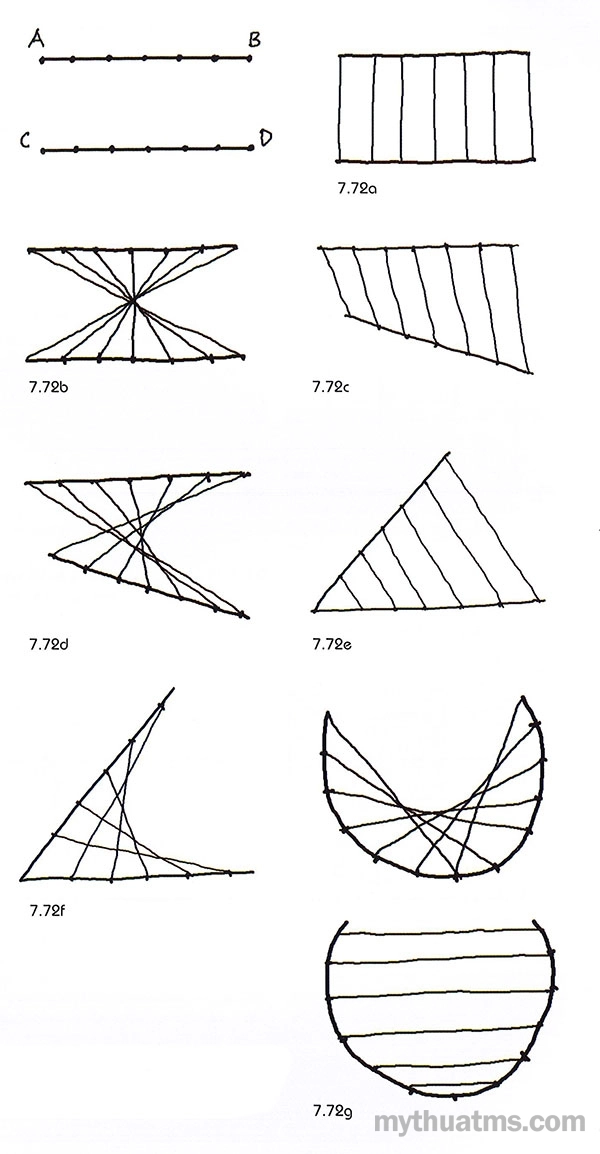
Hình 7.72: Biến thể tuyến liên kết khung cơ bản trên mặt phẳng

• Hai khung cơ bản song song với nhau, tuyến liên kết được đấu kết kiểu trực giao (hình 7.72a).
• Hai khung cơ bản song song, tuyến liên kết kiểu đảo chiều 9 (hình  7.72b).
• Hai khung cơ bản không song song, lệch nhau. Các tuyến liên kết đấu nối tuần tự (hình 7.72c).
• Hai khung cơ bản không song song, các tuyến liên kết kiểu đảo chiều (hình 7.72d).
• Hai khung cơ bản nối liền nhau tạo thành đường gấp khúc. Tuyến liên kết đấu nối tuần tự (hình 7.72e).
• Hai khung cơ bản nối liền nhau tạo thành đường gấp khúc. Tuyến liên kết đấu nối kiểu đảo chiều (hình 7.72f).
• Khung cơ bản được kết thành đường cong đều. Tuyến liên kết đấu nối kiểu tuần tự và đảo chiều (hình 7.72g).

* Tuyến liên kết – khung cơ bản trong không gian ba chiều: Nếu lấy hình lập phương làm ô gốc không gian với các đỉnh là A, B, C, D, E, F, G, H thì hình này có 8 đoạn thẳng. Trên các đoạn sẽ đánh dấu các điểm với số lượng như nhau. Với hình hộp này sẽ có nhiều phương án chọn khung cơ bản và tổ chức các tuyến liên kết.

Ví dụ, đoạn thẳng AD và HG được chọn làm khung cơ bản, sẽ có hai phương án tạo tuyến liên kết như hình 7.73.

Trong không gian ba chiều, khung cơ bản có thể là tuyến thẳng, tuyến cong, tuyến ba chiều hay một dạng hình học cụ thể nào đó. Hình vẽ 7.74 là ví dụ về tổ chức khung cơ bản – tuyến liên kết trên cơ sở hình gốc là khối lập phương.

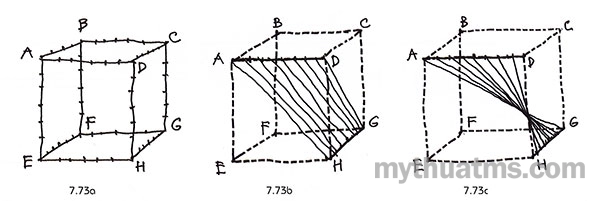
Hình 7.73: Hình lập phương và sơ đồ tuyến liên kết – khung cơ bản

a. Ô gốc lập phương có chia đoạn để hình thành tuyến liên kết trong không gian ba chiều.

b. Khung cơ bản là AD và HG, tuyến liên kết kiểu tuần tự.

c. Khung cơ bản là AD và HG, tuyến liên kết kiểu đảo chiều.

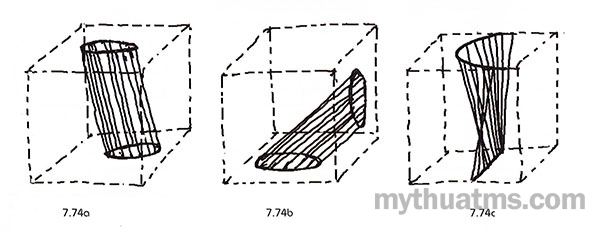
Hình 7.74: Các hình dạng khác nhau của khung cơ bản

a. Khung cơ bản có thể là hình tròn ở hai mặt phẳng song song đối nhau.

b. Khung cơ bản có thể là hình tròn ở hai mặt phẳng vuông góc nhau.

c. Tuyến liên kết có thể liên kết một khung cơ bản là đường cong tròn, một khung là đường thẳng.

BÀI THỰC HÀNH 7.6: Tuyến liên kết – khung cơ bản

Tổ chức dưới dạng mô hình một cấu trúc tuyến liên kết – khung cơ bản. Xem ví dụ hình 7.75 (bài tập sinh viên).

Hình 7.75: Tuyến liên kết – khung cơ bản

Hình 7.75a: Cấu trúc này khung cơ bản gồm một tuyến cong và hai tuyến thẳng. Hợp nhóm tuyến liên kết và khung cơ bản có vẻ tạo ra một không gian tương đối khép kín.

Hình 7.75b: Hai khung cơ bản có hình dạng tương đối tự do, cài giao thoa nhau tạo nên hệ khung chịu lực, cụt nhánh. Các tuyến liên kết đan cài phức hợp.

Hình 7.75c: Một rãnh xoắn, hai khung lẻ phụ trợ làm nên khung cơ bản. Các tuyến liên kết đấu nối xoay tỏa trên rãnh xoắn. Các tuyến phụ trợ tạo thêm vẻ đa dạng về hình cho tổ hợp.

Hình 7.75d: Một hợp nhóm khung và tuyến liên kết có tính chiều hướng rõ nhờ chuyển tiếp của các yếu tố thành phần qua dạng thức tuyến gấp khúc.

Hình 7.75e: Cấu trúc kiểu hướng tâm từ tám hướng thông qua tuyến và các bản diện chéo, phần trung tâm có sự biến động phi đối xứng tạo thêm vẻ đa dạng cho tổ hợp.

Hình 7.75f: Một bố cục đơn giản nhưng có hiệu quả thị giác thú vị, hai khung cơ bản xoay lệch nhau 90 độ, tuyến liên kết đấu nối chúng lại với nhau tạo nên bản diện cong hình rẻ quạt với nhiều vẻ khác nhau.

Hình 7.75g: Ở tổ hợp này có hai hệ tuyến liên kết bám bên trong khối kim tự tháp. Mỗi một hệ được trượt trên một cạnh cơ bản và đường chéo của đáy đã tạo nên hai mặt cong đối xứng nhau qua tâm đáy.

Hình 7.75h: Cấu trúc này có hai khung cơ bản đối nhau, một hình tròn, một hình đa giác. Tuyến liên kết đã tạo kiểu vặn xoắn cho khối nghịch lăng trụ.

Hình 7.75i: Một khung cơ bản là hình lập phương, các tuyến liên kết tổ chức đấu kết kiểu điểm với tuyến. Tổ chức cấu trúc kiểu giao thoa lặp lại và đối xứng.

Hình 7.75l: Có hai khung cơ bản là đường xoắn lệch nhau. Các tuyến liên kết đấu nối hai khung tuần tự, song song và trực giao, một bản diện cong vặn xoắn hình thành.

Hình 7.75k: Các khung cơ bản được đấu ghép với nhau kiểu cạnh tiếp xúc cạnh tạo ra chuỗi khung đa giác tương đồng. Các tuyến liên kết nội tại hợp nhóm kiểu tán xạ với tâm là điểm nối giữa hai khung cơ bản.

Hình 7.75m: Khung cơ bản hình lập phương được bổ sung thêm các cạnh chéo ở mặt cơ sở. Các tuyến liên kết đấu nối các cạnh chéo và cạnh cơ sở theo quy luật cân đối. Hợp nhóm được tạo ra tương đối phức tạp.

Hình 7.75n: Một khung cơ bản liền mạch kiểu xoắn ốc trụ, kết hợp tuyến liên kết tổ chức theo tuyến song song cách đều đã tạo nên các khe không gian kẹp giữa mỗi nhịp xoắn.

Hình 7.75p: Khung cơ bản hình lập phương được bao kín ba mặt. Ba mặt còn lại hở và khuyết một phần làm lộ ra hệ tuyến liên kết đấu nối theo ba cạnh thuộc ba diện khác nhau.

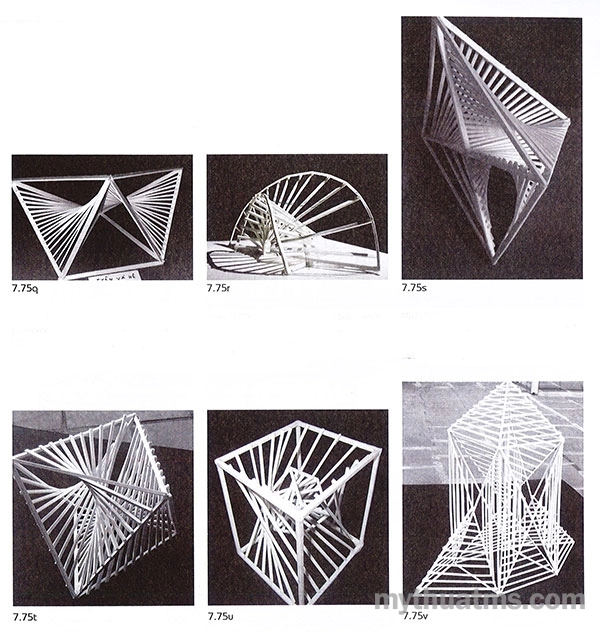
Hình 7.75q: Một khối đa diện nhiều mặt tam giác khung cơ bản. Hai hệ tuyến liên kết đối xứng tạo hai bản cong trong khối đa diện.

Hinfh7.75r: Hai hệ tuyến liên kết – khung cơ bản độc lập được tổ hợp theo cách cài lồng vào nhai. Một dạng dẻ quạt, một hình phễu.

Hình 7.75s: Một khung cơ bản hình kim tự tháp, diện đáy được chia làm bốn phần tạo nên bốn khung cơ bản các tuyến liên kết chuyển tiếp trong các khung này.

Hình 7.75t: Khối đa diện không đều làm khung cơ bản, bốn hệ tuyến liên kết tổ chức theo bốn kiểu khác nhau.

Hình 7.75u: Khối lập phương lớn chứa đựng khối lập phương nhỏ bên trong, hai khối không cùng chiều hướng. Một phần tuyến liên kết hai khối lập phương này.

Hình 7.75v: Một khối nghịch lăng trụ được tạo thành từ phức hợp tuyến liên kết và khung cơ bản.

7. Các lớp tuyến tạo không gian: Tất cả các khối hình tham tạo bởi diện phẳng và các bờ cạnh, tất cả các bản diện cong hay phẳng đều có thể chuyển thành dạng thanh (hình 7.76).

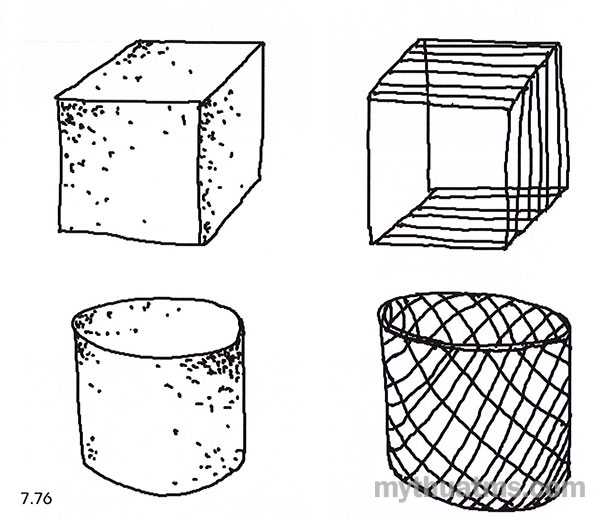
Một tổ hợp khối đặc, hay không gian có thể ít hấp dẫn về mặt thị giác vì nó bị che khuất cấu trúc bên trong, do vậy để tăng sức hấp dẫn và xử lí cấu tạo có thể chuyển thể trạng khối thành không gian dưới dạng thanh.

Các lớp tuyển tạo không gian là kiểu dạng tạo hình mà các thanh cong hay thẳng kết hợp với nhau theo quy luật để tạo ra một diện phẳng, diện cong hay một không gian cụ thể nào đó.

Kết cấu, cấu trúc dạng tuyến, dạng thanh được hợp nhóm theo cách biến đổi dần, theo phép lặp lại thường tạo nên vẻ uyển chuyển mềm mại. Hình 7.16h là ví dụ công trình kiến trúc sử dụng cấu trúc dạng này.

Cần lưu ý, trong nhiều trường hợp sự phân biệt giữa kiểu tổ chức “các lớp tuyến tạo không gian” và “tuyến liên kết – khung cơ bản” là không rõ ràng.

Sau đây là hai dạng thức cơ bản tổ chức các lớp tuyến tạo không gian.

a. Chồng xếp các hệ khung thanh định dạng: Ở dạng này các thanh liên kết thành một khung hình định dạng.

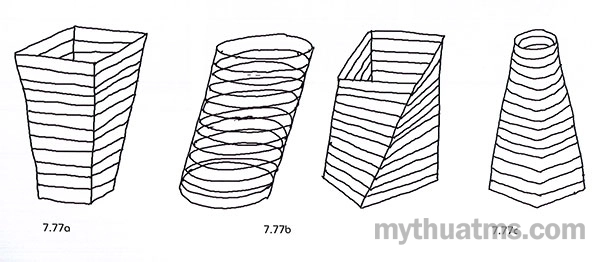
Khung này biến đổi theo cách:

• Thay đổi dần về kích cỡ (hình 7.77a).
• Xoay hay trượt hệ khung thanh (hình 7.77b).
• Thay đổi dần hình dạng hệ khung thanh (hình 7.77c).

b. Biến đổi các tuyến đơn:

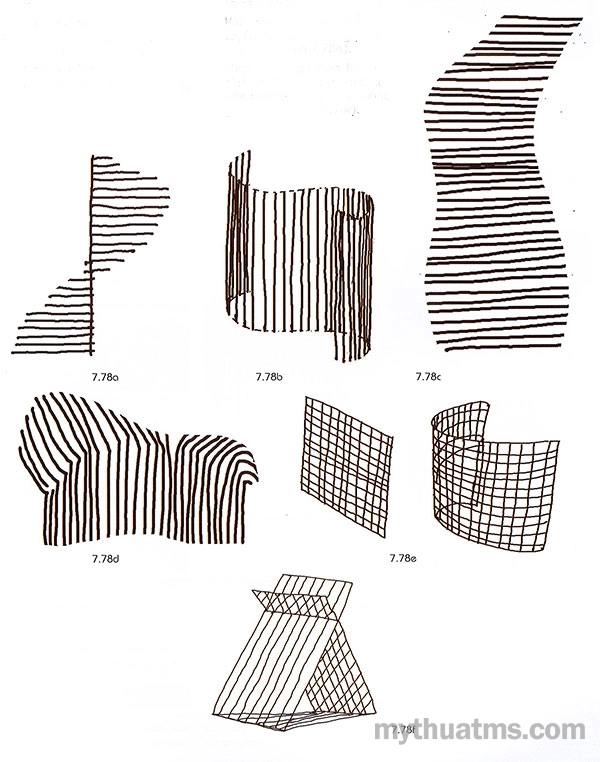
• Xoay quanh một tâm nào đó (hình 7.78a).
• Thay đổi vị trí, không thay đổi chiều hướng và hình dạng (hình 7.78b).
• Biến đổi dần về kích cỡ (hình 7.78c).
• Biến đổi dần về hình dạng (hình 7.78d).
• Kết hợp hai hay nhiều hệ tuyến để tạo ra mạng phẳng hay cong (hình 7.78e).
• Giao thoa, cài lồng hai hay nhiều hệ tuyến để tạo nên các mặt giao cắt nhau hay không gian cụ thể (hình 7.78f).

BÀI THỰC HÀNH 7.7: Các lớp tuyến tạo không gian

Tổ chức dưới dạng mô hình một bố cục tạo hình mang đặc tính không gian thông qua sử dụng các lớp tuyến – thanh. Xem ví dụ hình 7.79 (bài tập sinh viên).

Hình 7.79: Các lớp tuyến tạo không gian

Hình 7.79a: Khung thanh định dạng hình tam giác đều, biến đổi dần về kích cỡ, xoay đều quanh tâm hình tam giác.

Hình 7.79b: Một khung thanh định dạng hình tam giác với cạnh kéo dài, không thay đổi về kích cỡ hình dạng, cài lồng vào nhau. Các cạnh xoay đều quanh tâm đã tạo nên ba bán diện cong giao nhau vặn xoắn.

Hình 7.79c: Hình ảnh chụp nghiêng của hình 7.79b. Các bán diện vặn xoắn ba chiều thay đổi hình ảnh đối xứng khi nhìn từ trên xuống.

Hình 7.79d: Một cách tổ chức theo cách: không thay đổi hình dạng, chiều hướng chỉ thay đổi vị trí, hợp nhóm tuyến đã tạo ra ba bản diện độc lập.

Hình 7.79e: Một loại tuyến duy nhất, không thay đổi kích cỡ, chỉ thay đổi chiều hướng bằng cách xoay tỏa đều quanh trục.

Hình 7.79f: Hai hệ tuyến chuyển tiếp, tiếp xúc nhau tạo ra sự giao cắt ở phần cuối.

Hình 7.79g: Một kiểu khung – định dạng có hình tam giác các cạnh kéo dài không bằng nhau. Cũng có thể coi là ba hệ thanh giao nhau. Mỗi hệ xuất phát từ một thanh xoay quanh trục, mỗi trục này không giống nhau đã tạo ra ba bản diện cong giao cắt nhau.

Hình 7.79h: Các thanh có độ dài thay đổi dần, xoay dần quanh một trục.

Hình 7.79i: Một khung thanh định dạng với hai thanh vuông góc nhau, được biến chuyển theo cách: hình dạng không đổi, xoay đều quanh một trục ở vị trí đầu mút một thanh.

Hình 7.79k: Hai hệ tuyến giao cắt nhau theo góc nhọn. Mỗi hệ tuyến được hình thành từ hai các thanh đơn vị không đổi về kích cỡ, chỉ thay đổi về chiều hướng và vị trí.

Hình 7.79l: Hai hệ tuyến giao cắt nhau theo góc vuông. Một hệ là tập hợp các thanh không thay đổi về chiều hướng tạo ra bản diện cong. Hệ khác là các thanh thay đổi về chiều hướng nhưng tạo ra diện phẳng. Diện phẳng giao cắt diện cong.

Hình 7.79n: Một tập hợp các khung thanh định dạng tam giác và tuyến đơn tạo nên mạng ba chiều. Bố cục có một phần cấu trúc kiểu tuyến liên kết khung cơ bản.

Hình 7.79m: Bốn bản diện giao cắt nhau. Hai bản diện cong, hai bản diện phẳng.

Hình 7.79p: Một cách thức lặp lại hình dáng tuyến cong tổ hợp tuyến có tính cấu trúc không rõ ràng nhưng đồng nhất về hình dạng tuyến.

Hình 7.79q: Một phức hợp các bản diện phẳng được tạo từ các tuyến tổ chức kiểu đồng tâm giao cắt nhau.

Hình 7.79t: Các tuyến kết hợp tạo nên hệ mang ô lưới tam giác, tứ giác… Đây là cơ sở tạo ra các bản diện cong, vòm.

Hình 7.79r: Hai hệ tuyến tổ chức tương đối giống nhau. Các thanh đơn vị thay đổi dần về chiều hướng, chạy theo hai tuyến cong lồng vào nhau.

Hình 7.79s: Tất cả các bản diện cong hay thẳng đều có thể được cơ cấu từ hệ mạng. Hệ mạng trong hình được tạo thành từ sự giao cắt trực giao của các tuyến.

Hình 7.79v: Các lớp tuyến cong lặp lại về hình dạng, biến… dần về kích cỡ, chiều hướng không thay đổi đã tạo ra khối và lớp không gian có hình mềm mại mang dáng vẻ hữu cơ.

Hình 7.79u: Hai hệ tuyến tạo nên hai bản diện cong chung một bờ cạnh. Các tuyến cơ sở không thay đổi về độ dài, thay đổi dần về chiều hướng.

>>> Các dạng hình thể không gian (Phần 1)

>>> Các dạng hình thể không gian (Phần 2)

>>> Gợi ý cách tạo vật thể từ hình khối trong không gian (Phần 1)