Các dạng hình thể không gian (Phần 1)
1. Khối cơ bản:

Hình 7.18: Các khối cơ bản - Hình 7.19: Khối lập phương
Khối cơ bản (Primary Solids) gồm 5 khối: hình tháp (pyramid), hình côn (cone), hình cầu (sphere), hình lập phương (cube), hình trụ (cylinder), xem hình 7.18.
Kiến trúc sư Le Corbusier nhận xét về 5 khối cơ bản như sau: “Các hình lập phương, hình côn, hình cầu, hình trụ và hình tháp là những hình thể rất cơ bản. Hình ảnh của chúng luôn dễ nhận thấy và rõ ràng, không thể lẫn được trước ánh sáng. Đó chính là lý do chúng là những hình thể đẹp, đẹp nhất”.
a. Khối lập phương: Là loại khối đa diện đều được giới hạn bởi sáu mặt hình vuông. Do các mặt của khối là hình vuông đồng đều nhau nên có dáng vẻ chắc chắn, tĩnh lặng. Ở các góc nhìn khác nhau, khối lập phương luôn dễ nhận ra do các góc (đỉnh), các diện giống nhau. Nó luôn là hình thể ổn định về thị giác từ khi đứng tựa trên đỉnh hay một cạnh của khối. Khi khối lập phương bị cắt cụt đều đặn các góc ở đỉnh sẽ trở thành khối đa diện đều hoặc bán đều. Khối lập phương là cơ sở để chứa hai loại khối này. Xem minh họa hình 7.19.
Hình 7.19:
a. Khối lập phương được giới hạn bởi các mặt hình vuông giống hệt nhau. Khối lập phương chắc chắn và tĩnh tại nếu nằm trên bề mặt của khối. Khối trở nên có trạng thái động khi tựa trên một cạnh hay một đỉnh.
b. Khối lập phương khi bị cắt cụt đều đặn sẽ trở thành khối đa diện đều và bán đều. Trong ảnh là diễn tiến từ khối lập phương đến các khối (3.8.8); (3.4.3.4); (4.6.6) và (3.3.3.3).
b. Khối cầu: Khối cầu được hình thành từ sự xoay của nửa hình tròn quanh đường kính của nó. Khoảng cách từ bất kỳ điểm nào trên bề mặt khối cầu tới tâm đều bằng nhau. Khối cầu có đặc tính “độc lập”, định tâm, gây cảm giác cân bằng động khi đặt tiếp xúc trên một mặt phẳng. Nó lại có vẻ chắc chắn ổn định khi được ngập sâu vào mặt chứa nó. Từ bất kỳ điểm nhìn nào cũng thấy hình dạng tròn trịa của nó. Xem hình 7.20.

Hình 7.20: Khối cầu
a. Có đặc tính độc lập, định tâm.
b. Đặt trên một mặt phẳng.
c. Có vẻ chắc chắn khi ngập sâu vào mặt phẳng.
c. Khối trụ: Khối trụ được tạo ra do sự chuyển động của hình chữ nhật quay cạnh của nó. Khối trụ được giới hạn bởi một diện cong và hai diện phẳng. Tâm của hình trụ là trục định hướng hình, cũng chính là trục đối xứng của khối trụ. Khối trụ đứng vững khi đứng trên một mặt đáy tròn và có trục vuông góc với phương ngang. Khối trụ có vẻ bất ổn khi trục qua tâm có xu hướng nghiêng so với phương đứng. Khối trụ có trạng thái cân bằng động khi nằm ngang. Khối trụ có vẻ ổn định, chắc chắn khi một phần đáng kể của khối ngập trong mặt phẳng chứa nó. Khối trụ có thể dễ dàng phát triển kéo dài dọc theo tâm. Xem hình 7.21.

Hình 7.21: Khối trụ
a. Khối trụ đứng vững trên mặt phẳng đáy.
b. Khối trụ có vẻ bất ổn khi bị nghiêng đi.
c. Khối trụ có trạng thái cân bằng động khi nằm ngang.
d. Khối trụ có vẻ ổn định, chắc chắn khi ngập một phần trên mặt phẳng.
e. Khối trụ dễ phát triển kéo dài.
d. Khối hình côn (hay còn gọi là khối hình nón) được hình thành từ sự xoay của một hình tam giác vuông quanh cạnh góc vuông. Như vậy khối hình côn được giới hạn bởi hai mặt: một mặt phẳng tròn và một mặt cong. Chiều cao của khối côn không phụ thuộc vào đường kính của hình tròn đáy, nó có thể kéo dài dọc theo trục đối xứng của khối. Khối côn đứng vững, ổn định thị giác khi tựa trên mặt cơ sở hình tròn. Khối côn có vẻ bất ổn khi lật nghiêng hay đổ xuống. Khối côn mang vẻ cân bằng động khi tựa trên đỉnh hoặc một phần đỉnh ngập trong mặt phẳng chứa nó.

Hình 7.22: Khối côn
a. Khối côn đứng trên mặt phẳng tròn cơ sở.
b. Khối côn không ổn định khi lật nghiêng.
c. Khối côn mang vẻ cân bằng động khi tựa trên đỉnh.
d. Khối côn ổn định mang vẻ động khi đỉnh ngập một phần trong mặt phẳng ngang.
e. Khối hình tháp: Là khối đa diện được tham tạo bởi một đa diện cơ sở và các mặt tam giác. Các mặt tam giác gặp nhau tại một điểm (gọi là đỉnh). Chiều cao của khối tháp là khoảng cách từ đỉnh đến mặt đa diện cơ sở (gọi là đáy hình tháp). Đáy hình tháp không đều. Hình tháp đa giác đều là hình có đáy là đa giác đều và hình chiếu vuông góc của đỉnh với đa giác đáy trùng với tâm của đáy. Hình 7.23a là một số dạng khối hình tháp. Do tất cả các bề mặt của khối đều là mặt phẳng nên khối này ổn định vững chắc trên mỗi bề mặt của nó. Ở trạng thái này khối luôn góc cạnh và “cứng”. Khối tháp có vẻ bất ổn khi tựa trên đỉnh hoặc trên một cạnh của khối. Khối mang vẻ cân bằng động khi ngập sâu vào mặt phẳng ngang. Xem hình 7.23b.

Hình 7.23: Khối tháp
a. Một số dạng hình tháp.
b. Các trạng thái ổn định, bất ổn định của khối tháp.
Nhận xét chung về khối cơ bản: Khối cơ bản ít thấy trong tự nhiên vì vậy nó có vẻ kỳ dị khi xuất hiện với kích thước lớn (hình 7.24a). Bất kỳ một khối nào khi bị che khuất một phần chúng ta luôn có xu hướng tưởng tượng nó hoàn chỉnh dẫu rằng không nhìn thấy toàn bộ (hình 7.24b). Các khối cơ bản vừa ổn định vừa bất ổn định khi ở các trạng thái khác nhau (xem các hình 7.21; 7.22; 7.23).
Xử lý khối cơ bản:
* Khấu trừ khối: Có thể dùng thủ pháp khấu trừ hình thể (subtractive form) để xử lý khối cơ bản. Thủ pháp khấu trừ khối cơ bản có ưu điểm là khối bị khấu trừ một phần nhưng vẫn nhận dạng được khối gốc, vẫn đảm bảo được tính hình học thuần khiết của khối cơ bản. Tuy vậy, cần điều tiết mức độ khấu trừ sao cho đạt được sự hài hòa về tỷ lệ khi chia cắt các diện của khối. Việc khấu trừ nhiều có thể dẫn đến sự lập lờ về định danh khối và khó nhận dạng khối gốc.

Hình 7.24
a. Khối cơ bản ít thấy trong tự nhiên nên có vẻ kỳ dị khi xuất hiện to lớn, đầy đủ, toàn vẹn.
b. Khối cơ bản khi bị che đi một phần vẫn thấy như nó hoàn chỉnh.
Có các dạng khấu trừ sau:
- Phần khấu trừ khối chỉ xuất hiện trên bề mặt diện không làm thay đổi các bờ cạnh của khối (hình 7.25).
- Phần khấu trừ khối làm thay đổi một bờ cạnh và hai diện của khối (hình 7.26).
- Phần khấu trừ làm thay đổi nhiều bờ cạnh và nhiều bề mặt của khối (hình 7.27).
Hình 7.28 và 7.29 là các ví dụ trên mô hình và công trình kiến trúc dùng thủ pháp khấu trừ khối cơ bản để xử lý khối và tạo hình, tạo công năng cho kiến trúc.
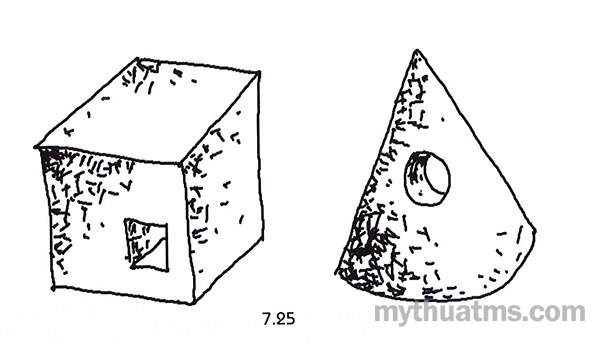
Hình 7.25: Khấu trừ khối chỉ làm thay đổi một bề mặt khối, các bờ cạnh khối không thay đổi

Hình 7.26: Phần khấu trừ làm thay đổi hai bề mặt khối và một bờ cạnh khối

Hình 7.27: Phần khấu trừ khối cắt qua nhiều diện và làm thay đổi nhiều bờ cạnh của khối

- Hình 7.28a: Khối lập phương bị khấu trừ từng phần nhỏ, phần khấu trừ vuông gốc với các diện, các bờ cạnh của khối gốc.
- Hình 7.28b: Phần khấu trừ chéo góc với bờ cạnh với diện và cắt qua bốn bờ cạnh của khối lập phương.
- Hình 7.28c: Một khối lập phương rỗng. Các bản diện của khối bị khấu trừ bởi các hình có các cạnh vuông góc hay song song với bờ cạnh khối gốc.
- Hình 7.28d: Một khối tứ diện bị khấu trừ ở ba đỉnh theo ba kiểu khác nhau.
- Hình 7.28e: Khối tứ diện bị khấu trừ bởi các lát cắt chéo so với bờ cạnh.
- Hình 7.28f: Khấu trừ khối bằng hai lát cắt chéo giao nhau, tạo ra phần khấu trừ không sâu nhưng mang vẻ khác lạ.
- Hình 7.28g: Khấu trừ khối lập phương theo cách đều đặn cân đối. Tạo ra kiểu dạng khối trong khối.
- Hình 7.28h: Khấu trừ bề mặt và đỉnh của khối lập phương kiểu giật cấp tạo nhịp.
- Hình 7.28i: Khấu trừ một phần nhỏ khối ở các đỉnh khối đặc. Các lát cắt vuông góc với diện cơ bản của khối.
- Hình 7.28k: Khấu trừ tạo ra tầng bậc. Một phần khấu trừ chạy dài gần hết khối gốc.
- Hình 7.28m: Khối lập phương rỗng phần khấu trừ tạo thành các vết dài song song hay vuông góc với bờ cạnh khối gốc.
- Hình 7.28n: Một phần khối lập phương được khấu trừ theo hai cách: lát cắt vuông góc và chéo góc với bờ cạnh khối gốc.
- Hình 7.28p: Bề mặt khối lập phương được khắc lõm và bo bờ, tạo ra yếu tố tuyến chạy bao quanh khối.
- Hình 7.28q: Các vết khấu vào khối có kích thước nhỏ, hình dạng tự do, trải đều trên diện, trên cạnh. Phần diện khấu trừ được kéo ra ngoài bề mặt khối.
- Hình 7.28r: Các vết khấu trừ chéo cạnh tạo ra bề mặt sinh động cho khối rỗng. Phần khấu trừ cắt qua nhiều bờ cạnh của khối.
Hình 7.28: Khấu từ khối cơ bản (bài tập sinh viên)

a. Family House, Stabio, Ticino, Switzerland, 1981: khấu trừ tạo khối trụ trong khối trụ (kiểu dạng: khối trong khối)…
b. Family House, Montagnola, Switzerland, 1989: khấu trừ một phần khối trụ theo các diện lớn nối liền nhau.
c. Family House Morbio Superiore, Ticino, Switzerland, 1983: khấu trừ một khối hộp chữ nhật, một mặt khấu trừ có hình chữ nhật, một mặt khấu trừ tạo khối trong khối.
* Cắt vát khối: Cắt vát khối là thủ pháp dùng một hay nhiều lát cắt để cắt khối cơ bản. Khối cơ bản khi được cắt vát có thể mang lại cho khối vẻ thanh thoát nhẹ nhàng hơn. Thủ pháp này hay được các kiến trúc sư sử dụng khi tạo bề mặt ngoài của công trình kiến trúc (xem các ví dụ hình 7.31 và 7.32). Lưu ý lát cắt có thể là phẳng hoặc hơi cong.
Có ba dạng cắt vát khối cơ bản: Lát cắt vuông góc với một hay hai diện cơ bản (hình 7.30a, b); Lát cắt vát chéo so với các bề mặt cơ bản của khối (hình 7.30c); Lát cắt trùng với bờ cạnh cơ bản của khối và có thể là giao nhau của hơn hai lát cắt (hình 7.30d).
Hình 7.29: Ba công trình của kiến trúc sư Thụy Sỹ Mario Botta dùng cách khấu trừ khối cơ bản để tạo hình kiến trúc

a. Lát cắt vuông góc với một hay hai diện cơ bản của khối gốc.
b. Lát cắt vát chéo so với các bề mặt của khối.
c. Lát cắt trùng với cạnh cơ bản của khối và có thể là giao nhau của hơn hai lát cắt.
Hình 7.30: Các dạng cơ bản cắt vát khối

a. Khối lập phương được vát chéo bốn bề mặt; bốn bờ cạnh hình khối chung đăng đối, trên to dưới nhỏ.
b. Các lát cắt vát chéo có cạnh trùng với cạnh cơ bản và giao nhau. Hình khối chung mang vẻ cân bằng động, vẫn có thể nhận dạng được khối gốc lập phương.
c. Kết hợp nhiều kiểu cắt vát: cắt vát chéo và giao nhau của hai lát cắt.
d. Một khối tháp tứ diện được cắt vát chéo theo nhiều kiểu: cắt vát trực giao, cắt vát chéo, giao nhau của hai lát cắt.
e. Khối lập phương rỗng được biến điệu thông qua giao của hai lát cắt lõm vào. Hai lát cắt trùng với hai cạnh cơ bản của khối.
f. Một khối lập phương được khoét, cắt vát bên dưới tạo vẻ phi cân bằng cho khối.
g. Phức hợp nhiều lát cắt trùng với bờ cạnh khối gốc tạo nên các gờ, múi. Xuất hiện nhịp giao thoa ở khối mới.
Hình 7.31: Các mô hình dùng thủ pháp cắt vát khối (bài tập sinh viên)


a) Walker Art Centrer expansion, minneapolis. USA. 2005. Herzog & De Meuron. Ba mặt phẳng có góc vát khác nhau chung bờ cạnh bao phủ bên ngoài công trình. Ánh sáng mặt trời chiếu trên bề mặt tạo sự khác nhau về mặt đậm nhạt, một phần khối công trình được khấu trừ đã tạo vẻ sinh động cho khối cơ bản.
b) Historisches museum Bern, Witzerland. 2012. Mlzd Architects. Các diện vát chéo có cạnh trùng với cạnh khối gốc. Chiều hướng các diện đảo chiều liên tục.
c) 41 Cooper Square - New York City. 2008. Morphosis. Các mặt vát (một phần hơi cong) cùng các khe kiểu khấu trừ khối đã tạo cho công trình vẻ uyển chuyển và bí ẩn.
d) The Art and Design School for University of moterrey in Mexico. 2013. Tadao Ando. Khối hình có vẻ bí ẩn, lạ lùng với các lát phẳng lát chéo, giao thoa.
c) Chia cắt khối và dịch chuyển
Hình 7.32: Các công trình kiến trúc sử dụng thủ pháp cắt vát khối để tạo hình
Một khối cơ bản có thể được chia cắt bởi các lát cắt. Khe chia cắt có thể có độ rộng lớn hay nhỏ. Khi khe chia cắt lớn sẽ có hiệu ứng như dạng khoét khối. Xem hình vẽ 7.33a.
Khối cơ bản sau khi chia cắt có thể được tổ hợp lại bằng cách dịch chuyển, xoay, trượt, tịnh tiến,... các phần đã bị chia cắt để tạo nên diện mạo mới. Thủ pháp này nhằm tạo ra một hợp nhóm khối sống động, có chức năng khác nhau ở mỗi phần nhưng vẫn nhận diện và hình dung được khối gốc nên có thể mang lại sự chắc chắn về tạo hình cho tổng thể. Hình 7.33b là sơ đồ minh họa chia cắt và dịch chuyển các phần chia cắt của khối. Hình 7.34 là một số bài tập về chia cắt khối và dịch chuyển.

Hình 7.33:
a) Một khối cơ bản có thể được chia cắt, khi nét cắt có độ rộng lớn sẽ có cảm giác khối bị rỗng, bị khoét khối.
b) Một khối cơ bản có thể trở nên sống động hơn khi bị chia cắt và các phần chia cắt được dịch chuyển thông qua xoay trượt, tịnh tiến,... hoặc cắt gọt bớt một phần.
Hình 7.34a: Một khối hộp được chia làm 5 phần nhờ các lát cắt song song. Các phần được dịch chuyển kiểu tịnh tiến theo một phương.


Hình 7.34b: Khối hộp được chia làm 5 phần nhờ các lát cắt song song. Các phần được dịch chuyển theo kiểu xoay có chiều hướng khác nhau kiểu rẻ quạt.
Hình 7.34c: Một khối hộp được xử lí theo ba cách cắt vát, khấu trừ và cắt khối; phần cắt được dịch chuyển bằng cách cắt vừa xoay vừa trượt.
Hình 7.34d: Một khối hộp được cắt đổi, tổ hợp lại bằng cách xoay một phần quanh trục của khối đã bị cắt.
Hình 7.34e: Một hộp chữ nhật cắt làm 5 phần. Các phần được tổ hợp lại theo cách xoay, trượt, thay đổi vị trí.
Hình 7.34f: Khối lập phương cắt thành 4 phần. Tổ hợp mới có các khối được xoay, trượt.
Hình 7.34g: Một khối lập phương được khấu hai lần theo kiểu đồng dạng. Tổ hợp mới được hình thành từ việc dịch chuyển, xoay các khối thành phần.
Hình 7.34h: Một cách tổ hợp khác của khối lập phương khấu trừ kiểu đồng dạng.
Hình 7.34i: Chia cắt và khấu trừ một khối hộp có các cạnh vắt chéo, góc nhọn với nhiều diện của khối có hình tam giác.
Hình 7.34: Chia cắt khối và dịch chuyển (bài tập sinh viên)
d) Khối cộng thêm: Thủ pháp cộng thêm khối hay các bản diện vào khối cơ bản giúp tổ hợp mới sống động, uyển chuyển và có tư thế phát triển hơn.
Các dạng cộng thêm khối cơ bản sau:
- Khối cộng thêm như được cài lồng, giao cắt với khối cơ bản. Các cạnh của khối cộng thêm thường nhỏ hơn bờ cạnh của khối gốc. Nhìn dáng vẻ chung, khối cộng thêm này như “ngập” vào khối gốc cơ bản. Xem sơ đồ hình vẽ 7.35.
- Khối cộng thêm có bề mặt tiếp xúc với khối gốc. Bờ cạnh khối cộng thêm có bề mặt tiếp xúc với khối gốc, với bờ cạnh khối gốc và thường nhỏ hơn. Xem sơ đồ hình vẽ 7.36.

Hình 7.35: Khối cộng thêm kiểu cài lồng giao thoa với khối cơ bản, khối như “ngập” vào và nhận dạng tương đối rõ hình dạng khối cộng thêm.

Hình 7.36: Khối cộng thêm tiếp xúc với khối gốc, khối này thường có cạnh nhỏ hơn và trùng với bờ cạnh khối gốc
- Khối cộng thêm có bề mặt tiếp xúc với khối gốc. Một số cạnh của khối cộng thêm có thể trùng với một số bờ của khối gốc. Hợp nhóm khối kiểu này có sự chuyển tiếp giữa khối gốc và khối cộng thêm nên dễ tạo sự uyển chuyển của khối hình. Xem hình 7.37.
- Khối cộng thêm kết hợp với khối gốc thông qua tiếp xúc bờ cạnh hay đấu các đỉnh với nhau. Xem sơ đồ hình 7.38.
- Khối nằm trong khối hay sự kết hợp khối đặc - khối rỗng. Xem hình 7.39.
Cần lưu ý, thủ pháp cộng thêm nới chung và khối cơ bản cộng thêm nói riêng là thủ pháp hay được dùng trong tạo hình kiến trúc bởi cách này phù hợp với kiểu không gian đa chức năng trong kiến trúc hiện đại, mỗi khối trong hợp khối thích ứng với công năng của riêng mình.
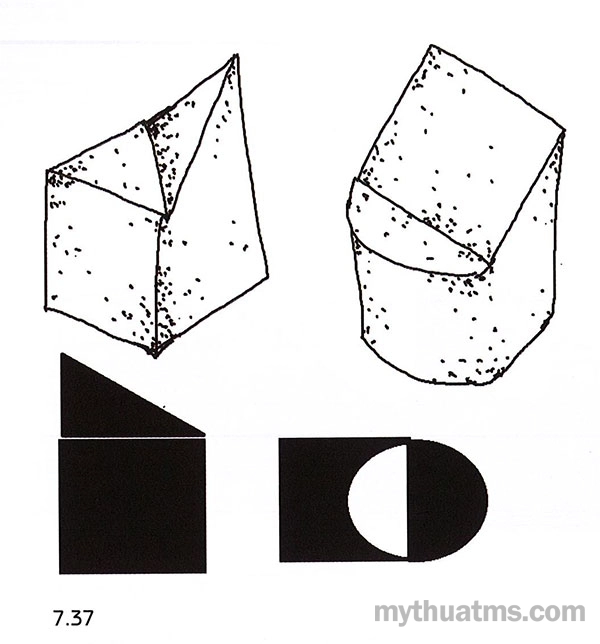
Hình 7.37: Khối cộng thêm tiếp xúc và có một số bờ cạnh trùng với khối gốc

Hình 7.38: Các khối kết hợp với nhau thông qua tiếp xúc cạnh hay đấu đỉnh

Hình 7.39: Khối trong khối hay sự kết hợp khối đặc - khối rỗng

Hình 7.40a: Các khối lập phương và hộp chữ nhật giao nhau, có các cạnh song song, đồng trục. Hợp khối tạo nên nhịp điệu.
Hình 7.40b: Ba khối giao cắt nhau, có chính có phụ, các khối không đồng trục. Hợp khối có trạng thái phi cân bằng.
Hình 7.40c: Hợp nhóm các khối rỗng và khuyết có kiểu thức giao thoa cài lồng. Các khối tập trung theo chiều đứng.
Hình 7.40d: Các khối lập phương tiếp xúc diện, chiều hướng mỗi khối không giống nhau. Hợp nhóm đậm đặc nhưng mở.
Hình 7.40e: Các cạnh của khối cộng thêm trùng với cạnh khối gốc. Hợp nhóm có sự chuyển biến nhịp nhàng, thay đổi chiều hướng.
Hình 7.40f: Một góc chụp khác cho thấy các bờ cạnh của khối cộng thêm trùng với cạnh khối gốc
Hình 7.40g: Hai khối tứ diện hợp nhóm với nhau theo kiểu tiếp xúc cạnh. Chiều hướng ngược nhau tạo thế cân bằng động.
Hình 7.40h: Hợp nhóm các khối tứ diện theo kiểu tiếp xúc diện, với sơ đồ tập trung theo tuyến cong.
Hình 7.40i: Các khối tứ diện hợp nhóm theo nhiều cách tiếp xúc cạnh, đấu đỉnh, thay đổi kích cỡ. Hợp nhóm kiểu tập trung vào một tuyến. Các diện tam giác xoay, đảo chiều liên tục tạo nên mảng sáng tối khác nhau. Cấu trúc mang vẻ hữu cơ.
Hình 7.40k: Một hợp nhóm khối rỗng, khối đặc, bản diện và tuyến kết hợp quanh một trục đứng. Dạng kết hợp kiểu tiếp xúc diện, đấu đỉnh, giao cắt khối. Hợp nhóm mang vẻ động và mở.
Hình 7.40l: Một hợp nhóm khối có các mặt tam giác kết hợp kiểu diện tiếp xúc diện, các cạnh trùng khít nhau. Các khối đa chiều hướng tạo tính biểu hiện.
Hình 7.40m: Hợp nhóm nhiều khối hộp chữ nhật rỗng và đặc - kiểu tiếp xúc diện và đồng hướng về khối. Tạo hình tầng bậc, vững chắc.
Hình 7.40 là các ví dụ dạng mô hình và hình 7.41 là một số công trình kiến trúc dùng thủ pháp khối cộng thêm khối - Hình 7.40: Khối cộng thêm (bài tập sinh viên)
Hình 7.40:
n) Kết hợp ba khối tháp kiểu cài lồng qua đỉnh. Chiều hướng ba khối giống nhau nhưng kích cỡ khác nhau. Lặp lại về hướng, lặp lại về hình dáng. Nhịp xuất hiện.
o) Các khối kim tự tháp kết hợp thông qua đỉnh. Khoảng đặc, rỗng xen kẽ xuất hiện hợp nhóm đăng đối tầng bậc.
p) Hợp nhóm khối tứ diện, khối nghịch lăng trụ và khối lăng trụ tam giác kiểu diện tiếp xúc diện. Hình khối chung mang vẻ động đa chiều hướng.
q) Kiểu kết hợp khối trong khối. Khối kim tự tháp nội tiếp bên trong trục cơ bản không trùng với khối lập phương.
r) Các khối lập phương hợp nhóm kiểu tập trung theo tuyến. Chiều hướng khối khác nhau, kích cỡ khác nhau, tiếp xúc kiểu cận kề, chồng xếp.



Hình 7.41: Kết hợp khối kiểu cộng thêm trong tạo hình kiến trúc
a. House in paco De Arcos, Lisbon, Porturgal. 2011. Jorge Mealha Arquitecto. Hợp nhóm các khối hộp theo kiểu cận kề nhau. Khoảng rỗng giữa các khối tạo vẻ thanh thoát thú vị cho công trình.
b. Team Disney Buiding, Orlando, Floida, USA. 1991. Arata Isozaki. Hợp nhóm nhiều kiểu dạng khối cơ bản. Kiểu khối trong khối, tiếp xúc khối, khối giao khối và có chiều hướng khối khác nhau. Hợp nhóm mang vẻ động và vui tươi.
Hình 7.41c: Kyoto Symphony Hall. Kyoto, Japan. 1992. Arata Isozaki. Khối trụ được các bản diện và khối lăng trụ tiếp xúc kiểu khối với các bờ cạnh trùng nhau. Công trình mang dáng vẻ uyển chuyển và hơi lạ lùng.
Hình 7.41d: The Cymbalista Synagogue and Jenish Heritage Center, Tel Aviv, Isael. 1996. Mario Botta. Hai khối phòng khán giả nổi cao là sự tiếp biến của khối hộp vuông và khối trụ. Đây là thủ pháp chuyển dạng diện dần, từ hình vuông sang hình tròn để tạo nên khối.
Hình 7.41:
e, f) Meseum of Contgemporary Art, Portugal, 1999. A’lvaro Siza. Hợp nhóm các khối hộp tiếp xúc kiểu khối, cài lồng khối và khấu trừ khối đơn lẻ. Công trình màn vẻ tĩnh lặng và bí ẩn.
g) Bảo tàng Van Gogh, Amsterdam (1998 - 2014). Kurokawa Kisho. Khối trụ được chia cắt làm hai, tương phản về chất liệu: đặc - rỗng, nặng - nhẹ.
BÀI THỰC HÀNH: Tạo hình khối cơ bản
Chọn từ 1 - 3 dạng khối cơ bản, kết hợp và xử lí các khối này theo các thủ pháp: khấu trừ khối, cộng thêm khối. Tổ hợp có thể ở dạng khối đặc, khối rỗng, hoặc kết hợp các bản diện cong hay thẳng, hoặc các tuyến. Tham khảo các hình 7.28, 7.31, 7.34 và 7.40.
>>> Độ sáng tối - đậm nhạt của hình thể