Ngôn ngữ của đối xứng

Hình 1
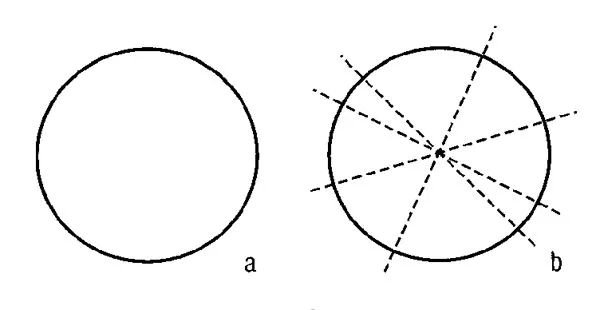
Một vết mực trên một mẩu giấy chẳng có gì đặc biệt bắt mắt cả, nhưng nếu bạn gấp đôi tờ giấy lại khi vết mực chưa kịp khô thì bạn sẽ nhận được một cái gì đó nhìn giống như hình 1 và rõ ràng là hấp dẫn hơn nhiều. Thực tế, việc giải thích những vết mực tương tự đã tạo cơ sở cho phép thử Rorschach do nhà tâm thần học người Thụy Sỹ, Hermann Rorschach, phát triển trong những năm 1920. Mục đích phép thử này được tuyên bố là để bằng cách nào đó làm sáng tỏ những nỗi sợ hãi ẩn giấu, những tưởng tượng điên dại và những tư tưởng sâu xa hơn của những người nhìn lý giải những hình dáng mơ hồ. Giá trị thực sự của phép thử này với tư cách là “tia X quang đối với trí óc” đã được tranh cãi gay gắt trong giới tâm lý học.

Hình 2: Sự ra đời của thần Vệ nữ của Botticelli
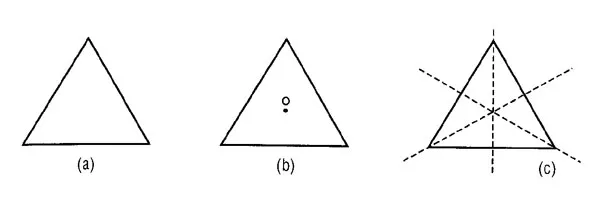
Đa số chúng ta cảm nhận những bố cục hài hòa như bức tranh Sự ra đời của thần Vệ nữ của Botticelli (Hình 2) như là một cái gì đó đối xứng. Nhà lịch sử nghệ thuật Ernst H. Gombrich thậm chí còn nhận xét rằng “cách hành xử khoáng đạt của Botticelli đối với tự nhiên nhằm đạt được những đường nét duyên dáng đã làm tăng thêm vẻ đẹp và sự hài hòa của “bức tranh”. Nhưng các nhà toán học sẽ nói với bạn rằng những bố trí màu sắc và hình dạng trong bức tranh đó là không đối xứng một chút nào theo nghĩa toán học. Trái lại, những người xem không phải là nhà toàn học lại không cảm nhận Hình 3 như là một cái gì đó đối xứng, thậm chí mặc dù nó thực sự là đối xứng theo định nghĩa hình thức của toán học. Vậy đối xứng thực sự là cái gì? Nó đóng vai trò gì (nếu có) trong sự cảm nhận của con người? Nó có liên quan như thế nào với cảm giác thẩm mỹ của chúng ta? Trong thế giới khoa học, tại sao đối xứng lại trở thành một khái niệm then chốt trong những ý tưởng của chúng ta về vũ trụ xung quanh và trong những lý thuyết cơ bản mưu toan giải thích vũ trụ đó? Vì đối xứng trải rộng trong nhiều lĩnh vực, chúng ta sẽ phải dùng “ngôn ngữ” gì và “ngữ pháp” nào để mô tả đặc trưng cho các đối xứng cùng các thuộc tính của chúng và cái ngôn ngữ phổ quát ấy đã được phát minh ra như thế nào?

Hình 3
1. Miễn trừ thay đổi:
Từ đối xứng (symmetry) có nguồn gốc từ xa xưa, xuất phát từ các từ sym và metria trong tiếng Hy Lạp, có nghĩa là “có cùng độ đo”. Khi người Hy Lạp gắn cho một tác phẩm nghệ thuật hay một thiết kế kiến trúc cái nhãn đối xứng là khi họ muốn nói rằng người ta có thể nhận dạng được một mẩu nhỏ nào đó của tác phẩm nghệ thuật ấy, sao cho kích thwocs của tất cả các phần khác đều chứa mẩu đó với một số lần rất chính xác (ác phần này được gọi là “thông ước” với nhau). Định nghĩa từ rất sớm này có lẽ tương ứng với khái niệm hiện đại của chúng ta về sự tỷ lệ hay cân đối hơn là với đối xứng.
Ý nghĩa hiện đại của đối xứng (lần đầu tiên được đưa ra vào cuối thế kỷ 18) theo nghĩa toán học chính xác thực sự là “sự miễn trừ đố với một thay đổi khả dĩ nào đó”.
Tất nhiên, ví dụ quen thuộc nhất của đối xứng phản xạ qua gương là đối xứng hai bên đặc trưng cho vương quốc các động vật. Từ các con bướm đến những con cá voi, từ chim cho tới con người, nếu như bạn cho nửa bên trái phản xạ qua gương bạn sẽ nhận được cái gần như đồng nhất với nửa bên phải.
Đối với nhiều người, từ đối xứng được mặc nhiên công nhận có ý nghĩa là đối xứng hai bên. Đối xứng hai bên thể hiện nổi bật trong thế giới động vật và khó có thể cho đó chỉ là ngẫu nhiên được. Thực tế, nếu bạn coi động vật là những tập hợp cực lớn của hàng ngày tỷ phân tử thì số các cách để xây dựng các cấu hình bất đối xứng sẽ cực kỳ nhiều hơn các cấu hình đối xứng. Các mảnh của cái bình vỡ có thể xếp theo nhiều cách khác nhau nhưng sẽ chỉ có một cách xếp duy nhất để cho các mảnh ăn khớp với nhau và tạo lại chiếc bình như nguyên vẹn (và thường có đối xứng hai bên).
2. Cấu trúc đỏng đảnh của tuyết:

Hình 4: Bông tuyết sáu góc
Ngoài đối xứng phản xạ gương ra, các bông tuyết còn có đối xứng quay: bạn có thể quay chúng theo những góc nhất định xung quanh một trục vuông góc với mặt phẳng của chúng (và đi qua tâm) thì chúng nhìn vẫn như cũ. Do những tính chất và hình dạng của các phân tử nước, các bông tuyết thường có 6 góc (hầu như) giống hệt nhau. Do đó, góc quay nhỏ nhất (trừ trường hợp khong quay gì cả) làm cho hình dạng của bông tuyết không thay đổi là góc quay trong đó mỗi đỉnh dịch chuyển được một “bước”.

3. Morris, Mozart và các cộng sự:
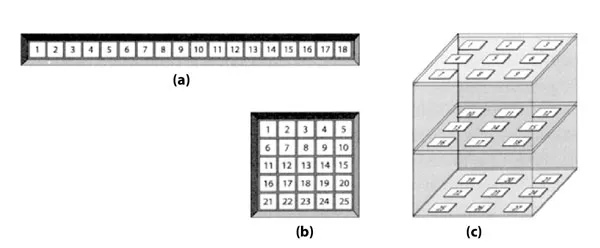
Một trong những hình ảnh mẫu đối xứng quen thuộc nhất là motif đệ quy lặp đi lặp lại. Từ những hoa văn trên các đền đài cổ và các hàng cột của các cung điện với những tấm thảm và thậm chí cả tiếng chim hót, đối xứng qua các hình mẫu lặp đi lặp lại luôn tạo ra một sự thân quen rất dễ chịu và một tác dụng an ủi tâm hồn. một ví dụ sơ cấp của loại đối xứng này là Hình 3.
Phép biến đổi đối xứng trong trường hợp này được gọi là phép tịnh tiến, nghĩa là dịch chuyển một khoảng cách nào đó theo một đường nào đó. Hình mẫu này được gọi là được gọi là đối xứng nếu nó có thể dịch chuyển theo các hướng khác nhau mà nhìn vẫn không thấy có sự khác biệt nào. Nói cách khác, những hình vẽ đều đặn mà trong đó một chủ đề được lặp đi lặp lại ở những khoảng cố định được coi được coi là có đối xứng tịnh tiến. Những hình trang trí có đối xứng tịnh tiến đã có từ 17.000 trước CN (thời đại Đồ đá cũ). Một chiếc vòng đeo tay làm bằng ngà voi ma mút được tìm thấy ở Ucraina có chạm một hình mẫu những đường gấp khúc lặp đi lặp lại. Những hình mẫu đối xứng tịnh tiên skhacs cũng được tìm thấy ở rất nhiều dạng nghệ thuật, từ gạch lát Hồi giáo thời Trung đại trong cung điện Alhambra ở Granada, Tây Ban Nha (Hình 10a) qua thuật in ấn thời Phục Hưng tới những bức tranh của họa sỹ đồ họa lập dị người Hà Lan M. C. Escher (1898-1972; hình 10b). Tự nhiên cũng đã cung cấp những ví dụ về các sinh vật có đối xứng tịnh tiến như con rết, trong đó các đoạn giống hệt nhau lặp đi lặp lại tới 170 lần.

Hình 10
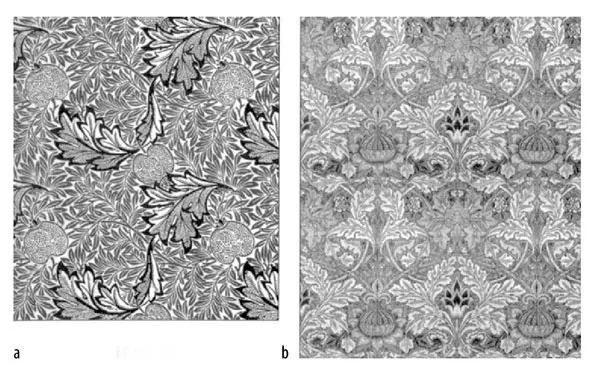
Hình 11
Họa sỹ, nhà thơ thời Victoria William Morris (1834-1896) là người đã sáng tác rất nhiều tác phẩm nghệ thuật trang trí. Nhiều tác phẩm của ông là sự thể hiện chính xác đối xứng tịnh tiến. Giai đoạn đầu đời, Morris đam mê kiến trúc Trung đại, và ở tuổi 27 ông đã lập một công ty trang trí mà sau này nổi tiếng dưới cái tên Morris và các cộng sự. Trong một phản ứng mạnh đối với trào lưu công nghiệp hóa đang rầm rộ ở nước Anh thế kỷ 19, Morris đã tìm cách để làm hồi phục nghề thủ công mỹ nghệ và làm sống lại sự huy hoàng của các nghệ thuật trang trí thời Trung đại. Morris và các cộng sự và sau này là Kelmscott Press được Morris thành lập vào năm 1890, đã thiết kế ra nhiều thứ gạch lát, khăn trải bàn, hàng dệt và những bản thảo được minh họa rất ngoạn mục theo Thiết kế Trung đại. Nhưng với thiết kế giấy dán tường, Morris lần đầu tiên đã đạt tới trình độ bậc thầy khó mà tưởng tượng được đối với các hình mẫu lặp đi lặp lại lại đối xứng tịnh tiến. Một vài chủ đề hoành tráng cảu ông được minh họa trên hình 11. Trong khi những đồ hình của Morris không có gì đổi mới hơn so với các tác phẩm của những người đương thời với ông như Christopher Dresser hay A.W.N. Pugin, nhưng ảnh hưởng và di sản của ông là rất to lớn. Bản thân Morris quan tâm đến việc khuyến khích nghệ thuật và nghề thủ công chứ không phải toán học của đối xứng.

>>> Đối xứng trong nghệ thuật (Phần 1)
>>> Nguyên lý hàng lối, cân đối, tự do trong cơ sở tạo hình
>>> Nghệ thuật và Đồ họa Trúc chỉ