Tỷ lệ chiều cao lý tưởng bằng 7 – 8 đầu từ đâu mà ra?
Polykleitos xứ Argos (kh. 480/475 – 415 TCN) đã theo đuổi tỉ lệ lý tưởng trong các bức tượng ông tạc. Trên cơ sở các công thức toán học đơn giản, ông đã xây dựng một hệ thống các nguyên tắc thẩm mỹ đầu tiên về tỉ lệ cơ thể người, được gọi là canon. Hệ thống này chia cơ thể con người ra các phần khác nhau, và liên hệ với nhau theo một quy luật toán học nhất định. Mục đích cuối cùng là đạt được symmetria, tức sự đối xứng. Tuy nhiên symmetria trong quan niệm của nghệ thuật cổ điển Hy Lạp thời cực thịnh (khoảng t.k. V TCN) không chỉ là sự cân bằng và tỉ lệ mà còn bao gồm cả tương phản. Điển hình là bức tượng Doliphoros (tức Người cầm giáo) của Polykleitos, được coi là mẫu mực của tỉ lệ lý tưởng của cơ thể người, trong tư thế contrapposto, hay đối trọng, tức thế đứng dồn trọng lượng cơ thể lên một chân, khiến vai và tay vặn trên mặt cắt ngang khỏi trục từ chân lên hông.
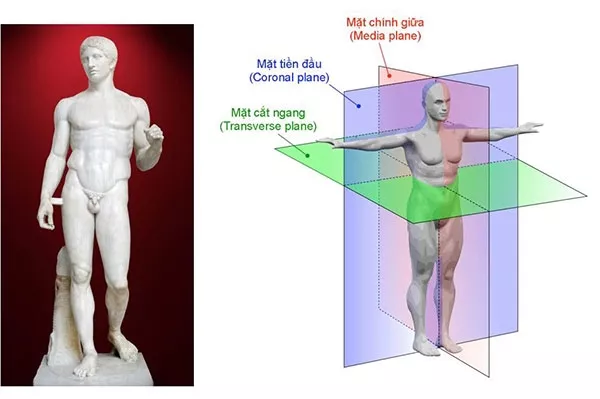
H.1 - Trái: Tượng Doryphoros, bản sao La Mã (kh. t.k. I TCN – t.k. I) từ bản gốc Hy Lạp, cẩm thạch, cao 2m.
Bào tàng khảo cổ quốc gia Naples.
Phải: Các mặt cắt trong giải phẫu cơ thể người: mặt cắt ngang (横断面: hoành đoạn diện, transverse plan hay axial plan),
mặt chính giữa (正中面: chính trung diện, median plane), mặt tiền đầu (前頭面: tiền đầu diện, coronal plane)
Pliny đã nhắc đến Polykleitos như sau: “Ông cũng đã làm bức tượng mà các nghệ sỹ gọi là tượng mẫu (Doriphoros - ND), bởi họ vẽ ra các đường nét nghệ thuật từ bức tượng đó như từ một thứ chuẩn mực; và ông là người duy nhất của nhân loại đã sáng tạo ra chính bản thân nghệ thuật chỉ bằng một tác phẩm nghệ thuật (…) Một phát minh hoàn toàn của ông đó là nghệ thuật làm các bức tượng dồn sức nặng lên một chân. Tuy nhiên, như Varro đã nhận xét, tất cả những hình người này đều được xây dựng theo hình vuông, và được làm theo cùng một mẫu.”[1]
Quy luật toán học Polykleitos đã dùng để xây dựng hệ thống tỉ lệ người lý tưởng của ông đến nay đã thất lạc và nhiều cố gắng khôi phục lại nó dựa trên tỉ lệ tuyến tính đều thất bại. Tới năm 1975 sử gia nghệ thuật người Mỹ Richard Tobin đã căn cứ vào các ghi chép cổ, ví dụ của Pliny nói trên, để khôi phục công thức xây dựng tỉ lệ người lý tưởng của Polykleitos dựa trên phép dựng hình vuông đơn giản, không cần dùng thước hay bất cứ phép tính nào [2]. Tobin phỏng đoán Polykleitos đã dùng đốt ngoài cùng của ngón tay út làm đơn vị (ví dụ bằng 1). Dựng một hình vuông có độ dài cạnh bằng độ dài đốt ngoài cùng của ngón tay út, Tobin suy ra độ dài của đốt giữa ngón tay út bằng đường chéo của hình vuông này, tức 1 x √2 ≈ 1.4142. Tương tự như vậy, đốt trong cùng của ngón tay út có độ dài bằng độ dài đường chéo hình vuông có cạnh dài bằng đốt giữa ngón tay út. Như vậy tỉ lệ độ dài giữa ba đốt của ngón tay út được xác lập theo tỉ số 1:√2. Lắp lại quy trình này cho ngón tay và bàn tay, Tobin suy ra xương bàn tay, tính từ gốc ngón tay út tới đầu xương cẳng tay, có độ dài bằng đường chéo hình vuông với cạnh dài bằng toàn bộ ngón tay út. Cẳng tay có độ dài bằng độ dài đường chéo hình vuông với cạnh dài bằng độ dài của bàn tay (tính từ đầu ngón tay út tới cổ tay). Tỉ số giữa chiều dài của cẳng tay, tính từ cổ tay tới khuỷu tay, và cánh tay trên, tính từ khuỷu tay tới khớp cùng của xương đòn (xương quai xanh), cũng bằng 1:√2.
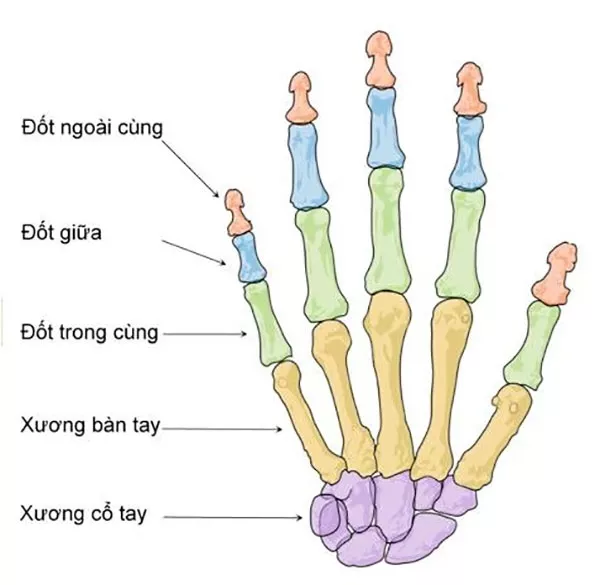
H.2 - Sơ đồ xương ngón tay, bàn tay và cổ tay
Sau khi thiết lập độ dài của cẳng tay bằng khoảng cách từ đỉnh đầu tới cằm (AB trong H.3) còn độ dài của cánh tay trên bằng khoảng cách từ đầu tới đỉnh xương ức (AC), ngang với khớp cùng của xương đòn (xương quai xanh), tỉ lệ của thân người cũng được tính từ đỉnh đầu xuống theo quy tắc tương tự, cụ thể là các tỉ số sau đây đều bằng đều bằng 1:√2,
- chiều cao của đầu (AB) : từ đỉnh đầu tới đỉnh xương ức (AC),
- từ đỉnh đầu tới đỉnh xương ức (AC) : từ đỉnh đầu tới đầu vú (AD),
- từ đỉnh đầu tới đầu vú (AD) : từ đỉnh đầu tới bụng (AE), trên rốn và ngang khuỷu tay,
- từ đỉnh đầu tới bụng (AE) : từ đỉnh đầu tới háng (AF), điểm chia đôi chiều cao của cơ thể người,
- từ đỉnh đầu tới háng (AF) : từ đỉnh đầu tới đỉnh xương đầu gối (AH),
- từ đỉnh đầu tới đỉnh xương đầu gối (AH) : từ đỉnh đầu tới gót chân (AJ), hay toàn bộ chiều cao của cơ thể người.
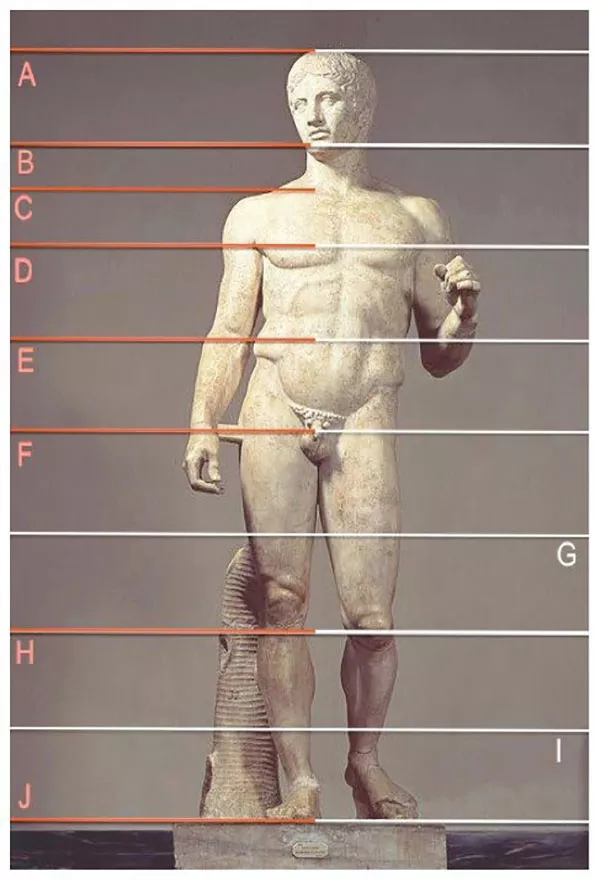
H.3 - Các phân khúc trên tượng Doryphoros theo quy tắc đường chéo hình vuông
Từ các tỉ số trên, có thể dễ dàng rút ra các tỉ lệ sau:
AB/AC = AC/AD = 1/√2, do đó AD = 2AB,
AD/AE = AE/AF = 1/√2, do đó AF= 2AD = 4AB,
AF/AH = AH/AJ = 1/√2, do đó AJ = 2AF = 4AD = 8AB.
Như vậy chiều cao lý tưởng của người đàn ông (AJ), theo quy tắc đường chéo hình vuông do Tobin phỏng đoán từ canon của Polykleitos, là bằng 8 chiều cao đầu người (AB). Trên thực tế, đầu tượng Doryphoros to hơn đầu trong tỉ lệ trên khoảng 1.14 lần (28.42 cm thay vì 24.9 cm trên chiều cao toàn thân 199.5 cm). Với kích thước đầu to hơn như vậy, toàn thân có chiều cao bằng 7 chiều cao của đầu.
Sau khi đã thiết lập được độ dài của
đốt ngoài cùng (ab),
đốt giữa (bc),
đốt đầu tiên (cd) của ngón út,
xương bàn tay (de),
cẳng tay (ef),
cánh tay trên (fg hay gA),
đầu (AB),
đầu – cổ/ức (AC),
đầu – vú (AD),
đầu – bụng (AE),
đầu – háng (AF),
đầu – gối (AH),
đầu – gót (AJ)
bằng cách thắt nút phân đoạn trên một sợi dây, chiều ngang tương ứng của cơ thể được phân đoạn trên một sợi dây thứ hai như sau. Dựng một hình chữ nhật có cạnh dài bằng ab, tức độ dài của đốt ngoài cùng ngón út, còn cạnh ngắn bằng chiều rộng của đốt đó. Sau đó đặt sợi dây thứ hai nằm theo đường chéo của hình chữ nhật đó xuất phát từ đỉnh a. Sợi dây thứ hai nằm trên đường chéo này lại được thắt nút phân đoạn thành ab’, b’c’, c’d’, v.v. Chiều ngang của các phần tương ứng trên cơ thể được xác đính bằng các đoạn thẳng bb´, cc´, dd´, ee’, ff’, gg’ (hay AA’), BB’, v.v.
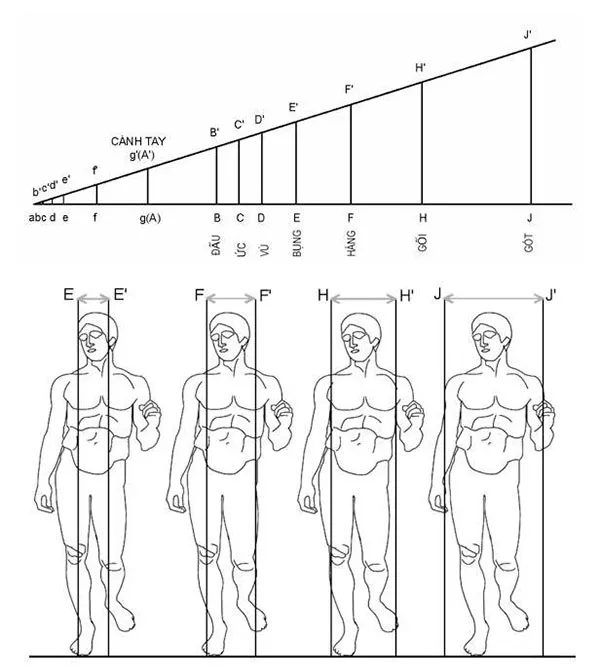
H.4 - Cách xác định chiều ngang ứng với chiều dài của các phân khúc trên cơ thể người trong canon của Polykleitos
theo phỏng đoán của Richard Tobin (Phỏng theo minh hoạ 8 và 14 trong công trình của R. Tobin).
Nhờ quy tắc đường chéo hình vuông nói trên, chỉ với hai sợi dây, điêu khắc gia có thể dễ dàng đánh dấu các đoạn thẳng bằng độ dài của các phân khúc trên cơ thể người đàn ông và các chiều ngang tương ứng theo canon của Polkleitos, xuất phát từ độ dài của đốt ngoài cùng của ngón thay út.

H.5.
Các kết quả tính toán của Tobin, theo quy tắc đường chéo hình vuông cho các khoảng cách trên bản sao tượng Doryhoros tại Bảo tàng quốc gia Naples, rất gần với số liệu đo thực tế của Kalkmann [3] (các số màu đỏ trong ngoặc đơn trong H.6) từ bản sao này (Sai số từ khoảng 0.3 – 4.2% ). Đó là một trong những minh chứng cho độ tin cậy của phỏng đoán của Tobin. Các tỉ số giữa hai số đo hai khoảng liền kề trên mặt tượng Doryphoros, ví dụ 28.4/20.9, 20.9/14.2, v.v., đều xấp xỉ bằng √2. Đối với các độ dài của các phân khúc trên cơ thể, sai số giữa các kết quả tính toán dùng quy tắc đường chéo hình vuông d Tobin phỏng đoán và số liệu đo thực tế chỉ vào khoảng 1%.
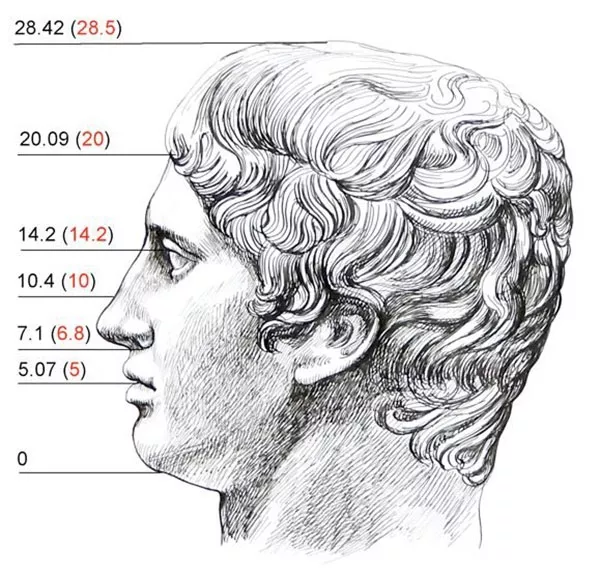
H.6
Các khoảng cách (cm) trên mặt Doryphoros được tính theo canon của Polykleitos do Tobin phỏng đoán (số màu đen, ngoài ngoặc đơn) và thực tế đo được từ bản sao La Mã của tượng này tại Bảo tàng quốc gia Naples (số màu đỏ, trong ngoặc đơn) (Minh hoạ của Nguyễn Đình Đăng, bút ngòi sắt và mực nho).
Sinh tại Sicyon vào khoảng năm 390 TCN, tức sau Polykleitos khoảng một thế kỷ, Lysippos đã cải tiến canon của Polykleitos bằng cách làm đầu người nhỏ đi và thân thon hơn, với chiều cao bằng 8 chiều cao của đầu.
Pliny viết về đổi mới của Lysippos như sau: “Những đóng góp chính của ông vàο nghệ thuật tạc tượng được cho là cách xử lý tóc rất sinh động, và làm cái đầu nhỏ hơn so với các tiền bối đã làm, với cơ thể thon hơn và bớt to hơn, khiến các hình người của ông trông cao hơn. Tiếng Latin không có từ nào thích hợp cho συμμετρία [4] (phát âm: symmet’ria), mà ông đã cẩn thận gìn giữ trong khi đưa vào quy tắc hình vuông của các tiền bối một sự đổi mới trước đó chưa ai từng nghĩ ra, và ông thường nói sự khác nhau giữa ông và các tiền bối là ở chỗ các tiền bối diễn tả con người như họ hiện hữu trên thực tế, còn ông diễn tả con người như họ được nhìn thấy. Đặc điểm chính của ông là cách thể hiện cực kỳ tinh tế, thậm chí tới những chi tiết nhỏ nhất.”[5]

H.7 - Trái: Tượng Doryphoros của Polykleitos có chiều cao bằng 7 đầu (Ảnh: CC BY 2.5).
- Phải: (Bản sao t.k. II) tượng Hermes ở Atalante của Lysippos có chiều cao bằng 8 đầu
Thế là, xuất phát từ canon của Polykleitos, được xây dựng hoàn toàn dựa trên nguyên tắc toán học trừu tượng, chuẩn mực về cái đẹp trong điêu khắc Hy Lạp cổ đại đã tiếp cận sự trung thành với tự nhiên (như được nhìn thấy bằng mắt) trong đổi mới của Lysippos, rồi nghệ thuật Phục Hưng sau này. Mặc dù quan niệm của Lysippos chính là quan niệm Plato đã phê phán, bởi nó chỉ diễn tả sự vật như được cảm nhận bằng thị giác chứ không phải bản chất của sự vật, đổi mới của Lysippos trên thực tế vẫn được điều tiết bởi nó được xây dựng trên nền tảng quy tắc toán học của Polykleitos. Vì thế khi các nhà nhân văn Phục Hưng như Alberti đề cao sự trung thực với tự nhiên, họ vẫn hàm ý đó là tự nhiên trên cơ sở các nguyên tắc toán học. Tự nhiên trong mắt người xem không thể thiếu sự chặt chẽ của các quy luật khoa học. Theo Tobin, canon của Polykleitos đánh dấu lần đầu tiên trong điêu khắc Hy Lạp cổ đại một nghệ sỹ đã thành công trong việc xây dựng một sự hài hòa hiếm hoi giữa các định luật của tự nhiên và các đòi hỏi chuyên môn của nghệ thuật.
- Nguyễn Đình Đăng -
>>> Vẽ đầu người theo PP xác định tỷ lệ
>>> Các quy luật liên quan đến tỷ lệ vàng
>>> Tỷ lệ trong thiết kế đồ gỗ và nội thất