Sự giao thoa của nghệ thuật và toán học
Một vài học giả cho rằng càng đi sâu hơn chuyên môn của mình, bạn sẽ càng hiểu rộng đến những lĩnh vực khác. Nếu đào sâu hơn về nghệ thuật và một ngày bạn lộ diện ở xứ sở Toán học, điều đó sẽ chẳng mấy ngạc nhiên đâu. Tessellations là một trong những đường dây giữa nghệ thuật và khoa học như vậy.

Thiên thần và Quỹ dữ – M.C. Escher – 1941
Tessellation là gì?
Khi các hình lặp lại, bao phủ một mặt phẳng mà không có khoảng trống hay bị chồng lắp, bạn có kết quả là một tessellation – họa tiết mosaic với hiệu ứng thị giác đê mê. Dù mỗi tessellation được sinh ra từ một bộ các quy tắc rõ ràng nhất quán của hình học và công thức – và ừm, trông nó có vẻ không phải sân chơi của những bộ óc sáng tạo – nhưng tessellations đã được chào đón bởi nhiều nền văn hóa, nhiều lĩnh vực trong cuộc sống, không trừ Thiết kế và Nghệ thuật.
Tessellations còn có tên khác là tiling – ốp lát, một tessellation có thể được tạo ra từ 1 hoặc nhiều hình cơ bản. Những đơn vị này gọi là ô gạch. Các ô gạch được xếp vào cạnh nhau như lát sàn nhà để hóa thành một công trình đồ sộ.
Chuyện thật bên lề, từ “Tessellation” có nguồn gốc Latin là tessellātus, có nghĩa là viên đá nhỏ hình vuông làm từ đá, đất sét hay kính, còn từ tiếng Hy Lạp là τέσσερα – tessera, nghĩa là “bốn”, cả hai từ này đều ngầm chỉ ra trò chơi xếp hình tessellation thuở sơ khai bắt nguồn từ việc xếp các ô vuông cạnh nhau – công thức cơ bản nhất để tạo ra các họa tiết tessellation.
Lược sử Tessellations:
Kỹ thuật tessellation được sử dụng trong nghệ thuật và kiến trúc, trang trí tường, mặt đường, trần nhà của nhiều công trình. Nguồn gốc của tessellation có thể là từ 4000 năm TCN, khi người Sumer sử dụng gạch đất sét trang trí trong nhà và đền thờ. Từ đó, tessellation tìm được chỗ đứng trong nghệ thuật của nhiều nền văn minh, từ Ai Cập, Ba Tư, La Mã và Hy Lạp, Byzantines, Ả Rập, Nhật Bản, Trung Quốc, Moors.

Một loại trang trí tường được sử dụng trong thời kỳ Utuk (TK IV – VI)
và Jemdet Nasr miền Nam Mesopotamia
Nhờ đó, kỹ thuật này trở nên rất đa dạng khi được phát triển và thích nghi trong nhiều nền văn hóa.
Thời Trung cổ đến thế kỷ 19, một nhóm trí thức bắt đầu quan sát và lý giải các cấu trúc hình học trong tự nhiên, theo sau là nhiều nghiên cứu liên quan, dẫn đến một sự phát triển của Tessellation thời kỳ sau đó cho đến tận bây giờ.
Tessellations và Hồi giáo:
Một trong những ví dụ thú vị nhất của kỹ thuật tessellation có thể tìm thấy trong nghệ thuật và kiến trúc Hồi giáo, đặc biệt trong nhóm dân cư ở Maghreb, Bắc Phi, Bán đảo Iberia, Sicily và Malta trong thời Trung cổ.
Hồi Giáo vốn dĩ cấm sử dụng các hình tượng sống trong nghệ thuật, vì thế concept hình học được chào đón như vị khách hoàn hảo. Sự trừu tượng của tessellation được chấp nhận một cách ngoạn mục bởi tôn giáo này.

Một tấm thảm Ushak – loại thảm đặc trưng của Thổ Nhĩ Kỳ
Ngoài cung điện Alhambra và các nhà nguyện, các hoa văn hình học và ốp lát cũng được sử dụng trong nghệ thuật trang trí như dệt may và đồ gốm. Những thiết kế này thường được gọi là “zillij” hay “zellige”, nghĩa là nghệ thuật trên nền tảng của sự học hỏi, kỷ luật và đức tin. Dựa trên những lời răn dạy trong đạo Hồi về một trí tuệ phổ quát chi phối toàn bộ cuộc sống, các nghệ sĩ zillij đã mô tả các quy luật của vũ trụ trong các tác phẩm bằng gạch nung phủ men. Dấu vết của nghệ thuật tessellation zillij vẫn có thể được tìm thấy ở Morocco và Algeria, trên các bức tường và sàn nhà, nhà thờ Hồi giáo, đài phun nước công cộng, lăng mộ, v.v.

Thánh đường Hassan II. @Werner Bayer
Tính Toán học của Tessellation:
Dù đã có thâm niên trong ngành nghệ thuật như đã trình bày ở trên, bí mật giấu sau lưng của tessellation lại là Toán học. Lý thuyết về tessellation rất rộng và phức tạp, thôi thì ta sẽ cùng nhau đi qua những điều cơ bản để làm quen với những tác phẩm nghệ thuật này.
Đầu tiên, cần điểm qua từ vựng kỹ thuật cơ bản:
- Fundamental region – vùng căn bản, hay gọi nôm na là ô gạch: là đơn vị hình được lặp lại để tạo ra tessellation.
- Edge – rìa/lề: đường tiếp xúc ở phần viền của 2 “ô gạch” – thường là đường thẳng.
- Vertex – đỉnh: điểm giao của 3 hoặc nhiều đường viền.
- Polygon – hình đa diện: một hình được tạo ra bởi ít nhất 3 đường thẳng và gốc, ví dụ đã biết: tam giác, tứ giác, ngũ giác,…
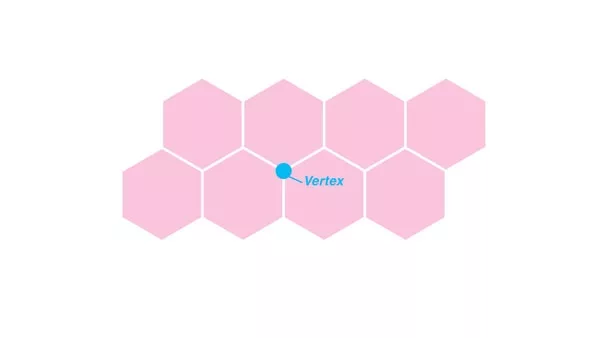
Với một số hiểu biết căn bản trên, mời bạn gieo mình vào biển rộng Toán học Tessellation.
Phân loại Cơ bản:
Một hình trong một ô gạch thì được gọi là prototile.
Xét về số lượng prototile được dùng, thì xếp hình chỉ có một prototile được gọi là ốp lát đơn – monohedral tiling. Tất cả các ô được sử dụng trong cách này đều đồng dạng với nhau. Cơ bản và nhàm chán nhỉ? Không đâu. Một ví dụ tessellation đơn đặc biệt thú vị là ốp lát đơn xoắn ốc được phát hiện đầu tiên bởi Heinz Voderberg vào năm 1936.

Xoắn đơn của chú Heinz Voderberg – tập trung cao độ nhé các cậu, chỉ có 1 prototile được sử dụng thôi đấy.
Ngoài đơn còn có đôi (dihedral tiling), tessellation này được hình thành từ 2 hình cơ bản. Tương tự, ta cũng có trihedral, tetrahedral và n-hedral, ứng với các tessellation ba, bốn, đa prototile.
Dựa vào loại hình học sử dụng, tessellation được phân ra là dạng đều (regular tessellation) , bán đều (semiregular) và không đều (irregular). Một tessellation có tính đối xứng cao là một tessellation được tạo ra từ các hình đa giác đều, cùng kích cỡ, tiếp xúc nhau từ đỉnh tới đỉnh.
Để gọi tên 1 tessellation đều hay bán đều, chúng ta hãy nhìn vào bất kỳ 1 vertex – đỉnh, đọc lần lượt con số tương ứng với số cạnh của khối hình học có mặt tại đỉnh đó.
Chỉ có 3 tessellation đạt được cảnh giới cao nhất này: đó là tessellation từ tam giác đều, hình vuông và lục giác đều.
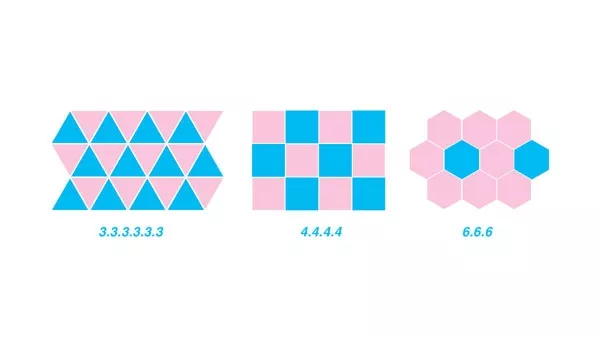
3 Tessellation đều và tên gọi
Số đo góc trong các prototile này đều là ước số của 360° , làm cho các prototile kề vai sát cách bên nhau khít không một khoản hở.
Một tessellation bán đều được tạo từ hai đa giác đều trở lên. Với loại này, khi bạn quan sát các đỉnh giao nhau, sẽ thấy cái prototile được lặp lại theo cùng kích thước và thứ tự.
Có 8 tessellation loại này được xào nấu từ các đa giác đều sau: tam giác đều, hình vuông, lục giác, bát giác và đa giác đều 12 đỉnh.
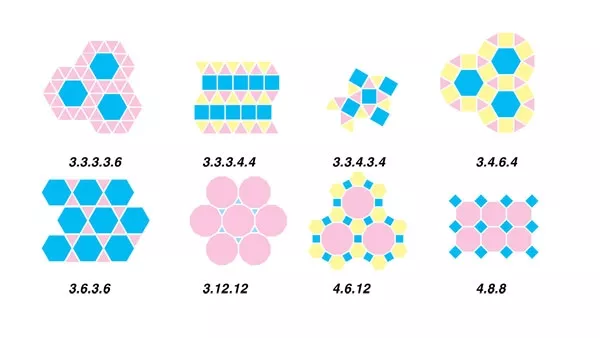
8 tessellation bán đều
Cuối cùng, Tessellation không đều không hạn định số lượng, loại hình và cả cách sắp xếp các thành phần xung quanh đỉnh giao. Số lượng tessellation loại này là một con số bao la.
Sự đối xứng và tổ hợp giấy dán tường:
Quan sát một tessellation hoàn thiện, bạn sẽ dễ dàng nhận ra có một bộ quy tắc chi phối nó. Khái niệm toán học thường gặp trong tessellation đó là tính đối xứng. Khác với định nghĩa đối xứng trục hay tâm trong một hình, tính đối xứng trong tessellations được gọi là đối xứng mặt phẳng (plane symmetries) hay sự dịch chuyển hình học (geometric transformations). Có ba loại đối xứng cơ bản trong mặt phẳng: tịnh tiến, xoay và lật.
- Tịnh tiến – translation: di chuyển đối tượng cùng 1 hướng với cùng 1 khoảng cách.
- Xoay – rotation: xoay đối tượng từ cùng một điểm, với cùng một góc.
- Lật – reflection: tạo ra một hình ảnh phản chiếu của một hình qua một đường thẳng. Một biến thể từ lật là glide reflection- lật – trượt: có được khi di chuyển hình phản chiếu dọc trục đối xứng thêm một đoạn.
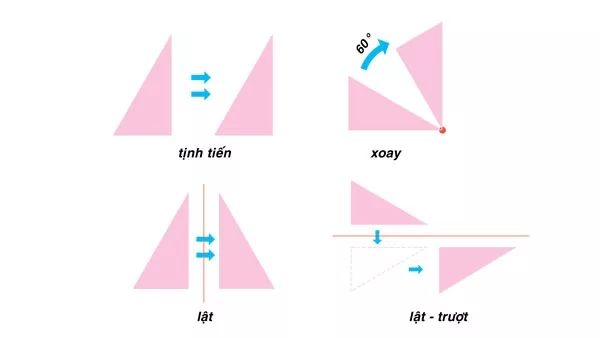
Ba dịch chuyển này gọi là isometric vì chúng không làm các ô gạch của tessellation thay đổi kích thước.
Ngoài ra, còn có một dạng dịch chuyển nữa làm cho kích thước ô gạch nhỏ/lớn dần đều. Nhiều nhà toán học không gọi đây là tessellation vì các ô gạch không còn bằng nhau và điểm cực giữa của hình thì không thể được lắp đầy.
Tessellations có thể được tạo ra bằng cách kết hợp nhiều cách dịch chuyển. Có tới 17 cách như vậy. Chúng được gọi là tổ hợp giấy dán tường (wallpaper groups). Số lượng chính xác cách sắp xếp họa tiết khả dĩ được đưa ra đầu tiên bởi Evgrad Federov vào năm 1891 và nó được chứng minh độc lập bởi một nhà toán học khác là George Pólya vào năm 1924. Nghiên cứu của Pólya đã truyền cảm hứng cho Escher. Dù không hiểu mấy khái niệm trừu tượng và công trình chứng minh trên, nhưng Escher đã đưa 17 quy tắc họa tiết đối xứng này vào thực tiễn và sáng tác ra 43 tác phẩm, nổi tiếng đến tận bây giờ.
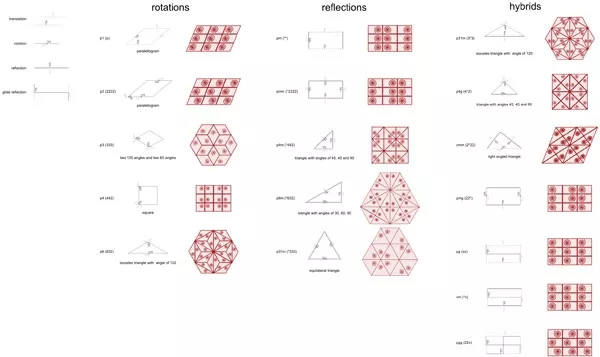
17 tổ hợp giấy dán tường
Cung điện Abraham ở Granada cũng được cho rằng chưa đầy đủ ví dụ cho 17 quy tắc này.
Ốp lát tuần hoàn và không tuần hoàn:
Tessellations có thể còn được phân loại dựa trên cách mà các ô đơn vị – unit cells, chứa một hoặc nhiều ô gạch. Nếu các ô đơn vị được sắp xếp lặp lại theo một thứ tự, tessellation đó được gọi là tuần hoàn – periodic. Tessellation tuần hoàn lặp lại một cách không giới hạn những ô gạch hoặc motif theo hai hướng tách biệt, và tạo ra họa tiết với tính đối xứng như 1 trong số 17 tổ hợp giấy dán tường trên.
Tessellation hình thành bởi họa tiết không lặp lại hoặc ngẫu nhiên được gọi là không tuần hoàn – aperiodic. Vì không thể lặp lại một cách vô tận, nên tessellation loại này có thể chỉ phủ kín một phần của mặt phẳng.
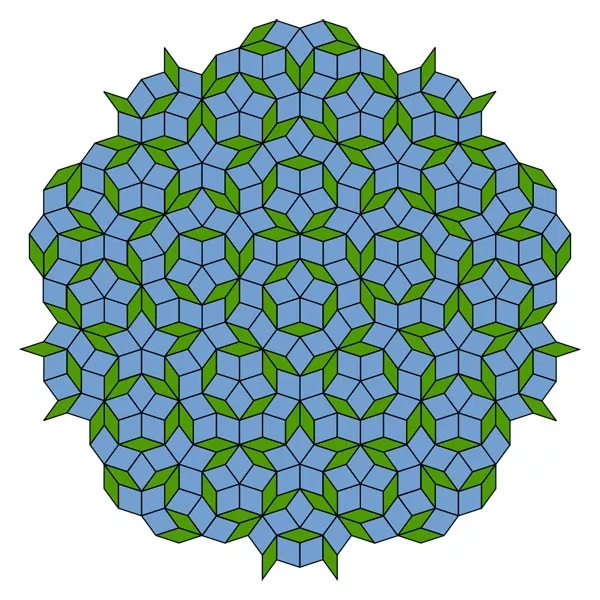
Tessellation Penrose
Một số ví dụ nổi tiếng nhất về tessellation không tuần hoàn là tessellation Penrose với hai hình tứ giác khác nhau, hay Pinwheel với những ô gạch xoay theo vô số hướng. Mặc dù trông có vẻ ngẫu nhiên, nhưng các thành ô đơn vị trong tessellation này vô cùng có quy tắc, ví dụ như quy tắc thay thế hoặc theo dãy số Fibonacci (tỉ lệ vàng).
Pinwhell Tessellation
Ví dụ khác về tessellations không tuần hoàn là Wang tiles gồm 1 nhóm 11 ô vuông có màu khác nhau ở các cạnh và sắp xếp theo một cách mà các cạnh chỉ gặp cạnh cùng màu với nó. Họa tiết này có thể phủ đầy một mặt phẳng, nhưng lại không có tính chu kỳ.
Ví dụ về Wang tiles nhắc đến khía cạnh màu sắc trong tessellations. Khi xem xét đến màu sắc trong tessellation, chúng ta cần quan tâm đến việc màu sắc được xem là một phần của kỹ thuật, hay chỉ là một phần trang trí thêm được thêm vào sau đó một cách ngẫu nhiên. Điều này quan trọng trong việc xác nhận xem các ô gạch cùng hình dáng nhưng khác màu có được tính là một đơn vị của tiling hay không. Điều này cũng quyết định đến việc xem xét tính đối xứng của tiling đó.
Tessellations trong chiều không gian cao hơn?
Đến đây chúng ta đã phủ đầy mặt phẳng 2 chiều với tessellation, nhưng liệu trong không gian 3D, họa tiết tessellation có xuất hiện? Một số khối đa diện, hoặc khối trong không gian 3D có thể xếp chồng lên nhau theo một để lấp đầy không gian 3 chiều. Một ví dụ tessellations trong các không gian đa chiều là các tổ ong – honeycombs. Với sự phát triển của các chương trình máy tính, chúng ta có thể tạo ra các tessellation trong không gian đa chiều với nhiều ứng dụng trong kiến trúc. Có một khả năng đáng quan tâm đó là việc kết hợp tessellation tuần hoàn và phi tuần hoàn trong kiến trúc.

Tessellation trong hình học phi Euclide?
Hình học phi Euclide là bộ môn hình học dựa trên cơ sở phủ nhận ít nhất một trong số những tiên đề Euclid. Hình học phi Euclid được bắt đầu bằng những công trình nghiên cứu của Lobachevsky (được Lobachevsky gọi là hình học trừu tượng) và phát triển bởi Bolyai, Gauss, Riemann.
Trong hình học Euclid, có duy nhất 1 đường thẳng đi qua 1 điểm cho trước và song song với 1 đường thẳng. Trong hình học phi Euclide, có ít nhất hai đường như vậy với hình học hyperbolic, còn trong hình học spherical thì không có hình nào. Vậy Tessellation có trong hình học phi Euclide không? Câu trả lời là có cho hình học hyperbolic. Trong hình học Euclide, có 3 loại tessellation đều và 8 loại tessellation bán đều, còn trong hình học hyperbolic, con số lên đến vô tận.

Hyperbolic tessellation từ plus.google.com và cgl.uwaterloo.ca
Tessellation và Nghệ thuật:
Tessellations đã xuất hiện khắp nơi trong hội họa, kiến trúc, thời trang, đồ họa, thủ công mỹ nghệ, v.v… cũng như khắp nơi về mặt địa lý, lịch sử, văn hóa.

Họa tiết sáp ong trên vải lanh nhuộm chàm người Mông, Việt Nam – nguồn: vca.org.vn
Tessellations là sự giao thoa của khoa học, toán học và nghệ thuật. Chúng ta thường có những đường ranh giới nhất định giữa nghệ thuật và phần lý trí, hay nghệ sĩ và các nhà khoa học. Nhưng ở một không gian lao động sáng tạo khác, các nghệ sĩ đã làm mờ và hòa tan khoa học cùng nghệ thuật trong những tác phẩm của mình.
Chẳng thể phủ nhận tính lặp lại, hình khối hình học và sự đối xứng là một thành phần của những tác phẩm đáng ngợi ca nhất trong lịch sử sáng tạo của con người hay nghệ thuật đương đại.
- Dịch, tổng hợp và minh họa: Liu May -
>>> Hội họa toán học của M.C.Escher
>>> Vẻ đẹp toán học trong nghệ thuật