Tạo hình ba chiều
Thế giới hình dạng, hình ảnh hai chiều nhiều khi trừu tượng và có tính chất tượng trưng, nó khác nhiều so với các vật thể là khối và không gian tiếp xúc hằng ngày.
1. Tạo hình hai chiều: Không gian hai chiều về bản chất do con người tạo ra. Ví dụ: Bản vẽ kĩ thuật, bức họa, tranh ảnh,... Nhiều khi chúng ta cảm nhận “như thật” và thấy thú vị một không gian ba chiều thông qua ước lệ của một hình vẽ phẳng hai chiều.
Khi sắp xếp các phần tử, các kí hiệu, các hình vẽ trên một mặt phẳng hai chiều nhằm hướng tới sự hài hòa về mặt thị giác, một logic về tạo hình nào đó tức là tạo hình hai chiều.
* Cảm nhận khối và không gian ba chiều: Chúng ta thực sự chỉ sống trong không gian ba chiều. Trong không gian này, ta cảm nhận các hiện vật. Nhìn phía xa, ngoái lại sau, nhìn sang phải, sang trái để tri giác và cảm thụ các vật thể. Tuy nhiên sự hiểu biết về khối, các vật thể khác trong không gian ba chiều không thể chính xác và thấu đáo khi nhìn vật thể từ một góc nhìn cố định.
Ví dụ: Một hình tròn trong không gian ba chiều có thể được cảm nhận là khối cầu, hình tròn, hình elip. Một tuyến song song với mặt đất, rất khó xác định chiều hướng của nó (xem hình 7.1).
Trong không gian ba chiều, để có thể hiểu một vật thể cần phải nhìn nó ở nhiều góc khác nhau, nhiều khoảng cách khác nhau, thậm chí phải xem xét chúng cả khi ở trạng thái động.
* Tạo hình ba chiều: Mục đích của tạo hình ba chiều giống như tạo hình hai chiều, là hướng tới sự hài hòa và trật tự thị giác, nhằm tạo nên hình thể có cấu trúc thú vị, hợp lí ở không gian ba chiều. Do vậy cần lưu ý:
- Xác định hiệu quả cảm thụ thị giác hình thể ở các góc nhìn khác nhau.
- Trong điêu khắc, kiến trúc và các tạo tác vật dụng, người ta thường làm trước phác thảo hay lập nên hệ thống bản vẽ với các hình chiếu bằng, chiếu đứng, hình vẽ phối cảnh, và mô hình, song song các bản vẽ, các mô hình ở tỉ lệ nhỏ khi lưu ảnh trên võng mạc sẽ khác nhiều so với hình dáng, kích thước thật trong thực tế. Do đó người thiết kế cần có cảm nhận đúng về kích thước thật của tổng thể cũng như các chi tiết của tác phẩm trong không gian ba chiều thông qua hệ thống các bản vẽ, phác thảo có tính ước lệ này.
- Một vật thể trong không gian ba chiều luôn được treo, đỡ, không thể lơ lửng trong không gian. Vì vậy cùng một vật thể hay một nhóm vật thể đã được hoàn thiện thì xác định vị trí điểm đặt ở đâu, tính chiều hướng ra sao, ngữ cảnh quanh nó như thế nào là quan trọng. Điều này ảnh hưởng tới sự ổn định, tính cân bằng, sự cảm thụ thị giác và tính thực dụng trong không gian ba chiều. Hình 7.2 cho thấy vị trí, chiều hướng khác nhau của khối lập phương sẽ có tính ổn định rất khác nhau.
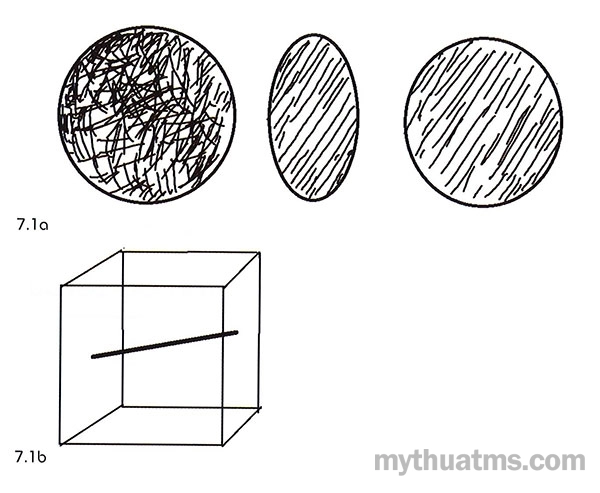
Hình 7.1: Cảm nhận hình thể trong không gian ba chiều
a. Một hình tròn trong không gian có thể bị nhầm là khối cầu, hình elip.
b. Một tuyến trong không gian ba chiều khi nó song song với mặt đất, rất khó xác định hướng xoay của nó.
* Mối liên hệ giữa tạo hình hai chiều và ba chiều: Nền tảng của việc tạo tác chiều thứ ba của vật thể (khối, không gian) được hình thành từ sự phối kết các diện, các tuyến. Diện xác định không gian, xác định khối tích. Nếu coi nghệ thuật tạo hình ba chiều (điêu khắc, kiến trúc) là một ngành nghệ thuật thị giác quan trọng với thành phần cơ bản là khối và không gian thì diện được đánh giá là chìa khóa quan trọng nhất của tạo tác ba chiều. Một cách đơn giản để tạo ra một hình thể, một khối, một không gian ba chiều là dùng tổ hợp các đa diện hai chiều. Từ hình đa diện cơ bản này, trên cơ sở một mặt phẳng có thể dựng nên một khối.
Hình 7.3 cho thấy với một hệ mạng là tổ hợp các đa giác đều ở dạng diện phẳng dùng thủ pháp cắt, gấp sẽ cho khối đa diện đều và bán đều.
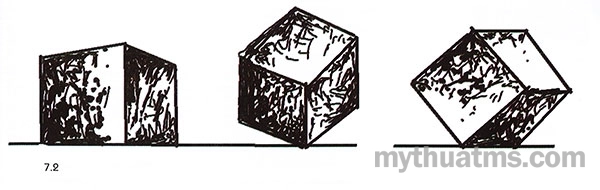
Hình 7.2: Tính ổn định trong không gian ba chiều
Với vị trí, điểm đặt khác nhau, khối hình lập phương sẽ cho sự ổn định khác nhau.
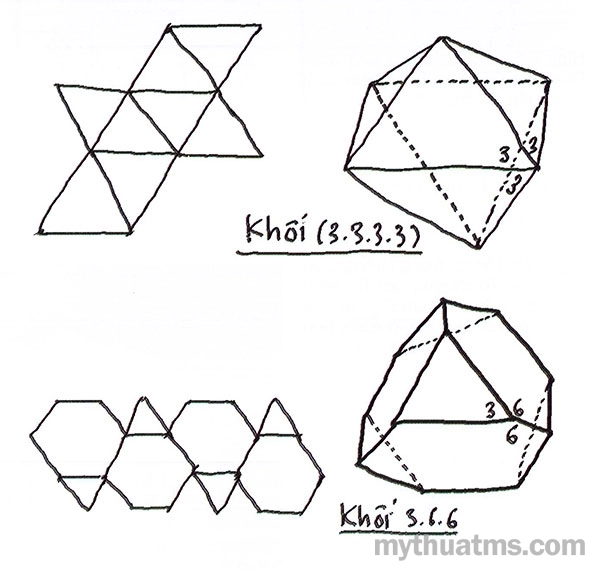
Hình 7.3: Từ diện phẳng, trên cơ sở mạng đa giác đều, bằng phương pháp
gấp đã tạo ra khối đặc
a. Khối bát diện (khối 3.3.3.3) được hình thành từ tám diện giác đều bằng nhau.
b. Khối tứ diện cụt (khối 3.6.6) được hình thành từ hai loại đa giác đều tam giác và lục giác.
Hình 7.4 là bài tập của sinh viên. Dùng diện phẳng thông qua cách gấp, uốn để tạo nên không gian và khối
2. Quá trình giải khối trong nghệ thuật tạo hình:
Thông thường chúng ta quan niệm khối là vật thể với ba chiều kích thước. Nó tồn tại trong không gian ba chiều. Ta thường gọi là “ khối đặc” hay “tượng tròn”. Các bề mặt của khối thường là cong hay phẳng đều. Ít có “hố thủng”, “vết lõm” lớn (xem ví dụ hình 7.5).
Có không gian hữu hạn, không gian vô hạn, không gian xác định và không gian vô định, nhưng không có khối vô hạn và khối vô định. Khối là vật thể có giới hạn, có khối tích nhất định.
Tuy nhiên, khái niệm về khối trong quá trình phát triển của điêu khắc, và design thị giác (visual design) luôn thay đổi. Những khái niệm khác nhau đã mở cho các nghệ sĩ tạo hình những khoảng biên rộng lớn để truyền tải các thông tin và tình cảm.

Hình 7.4: Diện tạo không gian và tạo khối (bài tập sinh viên)
a,b. Diện tạo không gian.
c. Diện tạo khối lăng trụ khuyết.
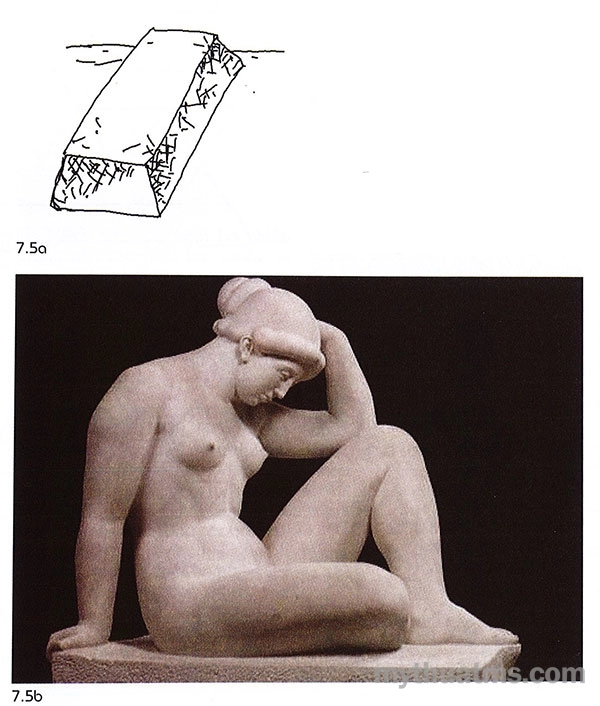
Hình 7.5: Khối đặc có các bề mặt cong hay phẳng đều
a. Một khối hộp đặc.
b. Một “tượng” tròn của Aristide Maillol.
Khái niệm khối xét về mặt cấu tạo (Composition), cấu trúc (Structure) dần dần tiếp cận và hòa nhập vào khái niệm không gian. Có một số vấn đề và khái niệm quan niệm, cần lưu ý:
a) Khối rỗng
Một khối đặc khi chiếm chỗ trong một không gian quanh nó chính là “khối rỗng”. Ví dụ xem sơ đồ hình 7.6.
b) Khối lồi, khối lõm (khối dương , khối âm)
Một khối bất kì, nếu mặt của khối lồi ra như chịu sự tác động từ trong và mặt cong hướng ra ngoài, được gọi là khối lồi hay khối dương.
Một khối diện cong lõm vào trong như chịu sự tác động từ bên ngoài vào, được gọi là khối lõm hay khối âm (xem hình 7.7).
Một mặt cong lõm hay lồi sẽ có sức căng bề mặt càng lớn khi độ cong tăng lên. Khi góc độ cong càng lớn tới mức di chuyển sang dạng gấp khúc hay dồn ép tụ theo điểm thì sức căng thị giác rất lớn (hình 7.8). Điều này giải thích tại sao những khối hình có các diện gấp đột ngột, các khe rãnh lồi lõm thường có cảm giác về sự chuyển động và tính biểu hiện mạnh mẽ về hình thể.
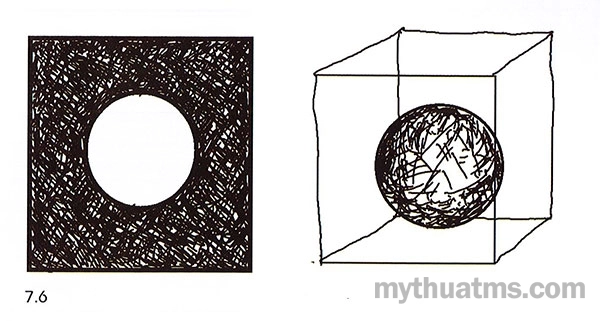
Hình 7.6: Khối rỗng
Khoảng không gian của một hình cầu đựng trong một hình lập phương là một dạng khối rống - khối âm.
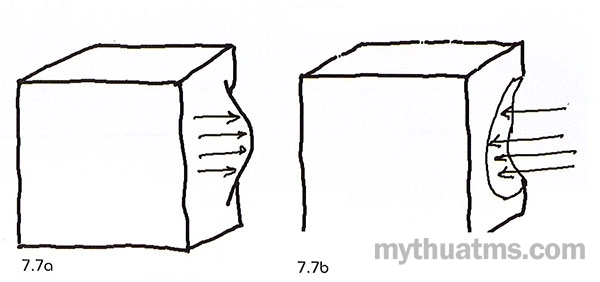
Hình 7.7: Khối âm, khối dương
a. Một khối có mặt của khối lồi ra như có lực tác động từ trong gọi là khối lồi hay khối dương.
b. Một khối có mặt lõm vào trong như chịu sự tác động từ ngoài vào gọi là khối lõm hay khối âm.
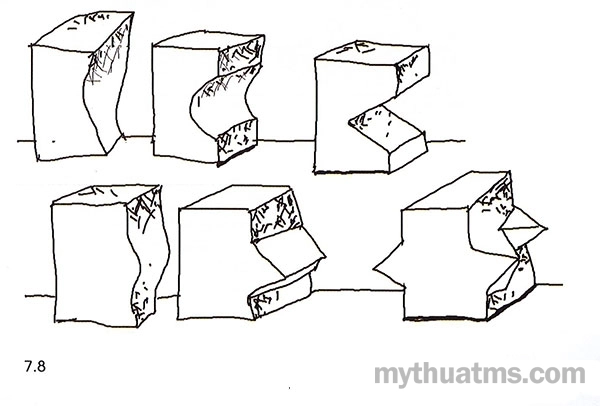
Hình 7.8: Sức căng thị giác của khối càng lớn thì các khe rãnh hay các đỉnh xuất hiện
từ sự giao cắt của các diện có góc độ hẹp
Hình 7.9 là hai tác phẩm điêu khắc hiện đại dùng thủ pháp khối lồi, tạo mảng lõm. Một của Umberto Boccioni theo phái Vị lai (Futurism). Một của Ossip Zadkine theo phong cách tập thể (Cubism).

Hình 7.9: Điêu khắc dùng khối lồi, khối lõm
a. Umberto Boccioni. Unique form of continuity in space. 1913. Các diện cong lõm, cong lồi, các diện giao cắt uốn lượn biểu hiện sinh động của cơ thể.
b. Ossip Zadkine. Woman standing. 1992. Các diện cong lõm cùng phần lồi của khối tròn tạo ấn tượng về sự sống động, chắc khỏe.
c. Khối khấu trừ:
Một khối cơ bản hay một khối bất kỳ có thể biển đổi theo cách khấu trừ đi một phần. Mức độ trừ đi có thể nhiều hay ít.
Thường khối khấu trừ (Subtractive Volume) bị trừ một phần và tạo nên ý nghĩa mới nhưng vẫn giữ được vóc dáng chung và sự ổn định ban đầu. Việc trừ đi nhiều có thể dẫn tới biến đổi khối thành nhóm loại hình khác, ví như khối rỗng, khối ước lệ.
Hình 7.10 là hình vẽ khối lập phương bị khấu trừ và một công trình được tạo hình theo cách khấu trừ khối, một thủ pháp hay được dùng trong kiến trúc.

Hình 7.10: Khấu trừ khối - khối khấu trừ
a. Hình lập phương bị khấu trừ.
b. Walker Art Center espansion, min Neapolis, 2005. Herzog & De Meuron. Công trình kiến trúc được tạo hình theo cách khấu trừ một phần khối đặc. Tính vững chắc được bảo tồn nhưng vẻ sinh động xuất hiện.
d) Khối cộng thêm: Một khối cơ bản hoặc một khối bất kì có thể được biến đổi theo cách cộng thêm (ghép thêm) một phần phụ mà không lấn át khối chính.
Khối cộng thêm (addtive Volume) có thể có hình dạng giống hoặc khác khối gốc. Hình 7.11 là ví dụ hình vẽ khối lập phương được cộng thêm.
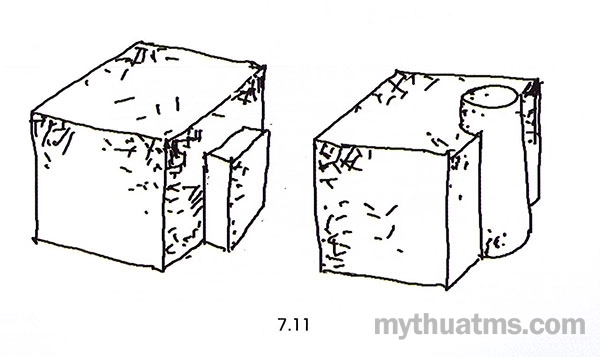
Hình 7.11: Khối cộng thêm
Hình lập phương được cộng thêm khối hộp chữ nhật và khối trụ. Các phần cộng thêm không ảnh hưởng nhiều tới việc nhận dạng khối gốc.
e. Khối rỗng - tính ước lệ của khối: Nếu phần rỗng, phần “âm”, phần khấu trừ của khối được nhấn mạnh, phần “dương” giảm thiểu. Khi đó, khối trở thành khối rỗng.
Khối rỗng có nhiều cấp độ về độ rỗng:
+ Rỗng một phần nhưng tồn tại phần diện và phần nhận dạng được rõ hình dạng chính của khối gốc. Xem ví dụ hình 7.12.
+ Mức độ rỗng nhiều hơn, một phần lớn khối bị rỗng. Xuất hiện yếu tố nét, diện mảnh. Người xem cần liên tưởng về hình ảnh khối gốc. Xem ví dụ hình 7.13.
+ Giới hạn khối rỗng chỉ còn là các biểu hiện đơn giản mang tính ước lệ. Xem ví dụ hình 7.14.

Hình 7.12: Khối rỗng một phần, vẫn nhận dạng được khối
a. Mạng và khối lập phương rỗng (bài tập sinh viên).
b. Henry More. Atom piece. 1964.
c. Henry More. Mother and child. 1963.

Hình 7.13: Chỉ còn đường nét, các diện mảnh làm liên tưởng tới khối đặc.
a. Ossip Zadkine. Destroyed City. 1953.
b. Alexander Archipenko. Walking woman. 1912.

Hình 7.14: Khối chỉ mang tính ước lệ. Khối được suy luận từ các tín hiệu thị giác đơn giản
a. Hợp nhóm hình lập phương (bài tập sinh viên)
b. Sol Lewit. Incomplete Open Cube No. 5 - 6.1974. Hình lập phương được xác lập do suy luận, tưởng tượng.
3. Nhận thức về cấu trúc và hình thể ba chiều: Thị giác chỉ có khả năng tiếp xúc và hiểu biết về hình thể (form) và không gian (space). Với các chiều khác nhau sẽ có không gian nhỏ hẹp, không gian hữu hạn và không gian rộng lớn, rất rộng lớn. Chúng ta sống, vận động trong đó. Các không gian này được xác định và khu biệt nhờ các vật thể hay cụ thể tồn tại bên trong.
Như vậy, để hiểu - nhận dạng và tạo tác không gian cần tiếp cận nhận thức về hình thể cùng các tác động ngoại vi khác (dưới góc độ vật lí và thị giác) lên hình thể.
Các nghiên cứu thuộc tính về mặt thị giác và cấu trúc của hình thể cần đề cập gồm:
1. Tìm hiểu dạng cấu trúc chung của hình thể (kết cấu hình thể).
2. Nghiên cứu các đặc tính thị giác của bản thân hình thể (đặc tính thị giác tự thân);
3. Xem xét các quan hệ tương quan giữa các hình thể với nhau và với không gian chứa chúng (quan hệ tương quan);
4. Nhận dạng cách tổ chức cấu trúc của một hay nhiều hình thể (tổ chức hình thể).
Đây là bốn vấn đề căn bản để nghiên cứu hoàn chỉnh một hình thể riêng lẻ và hình thể trong tổng thể chung.
1. Hình dạng cấu trúc chung: Xét dưới góc độ thị giác, kết cấu hay cấu trúc, thế giới của hình thể được chia làm hai dạng: kiểu khung xương và kiểu mảng khối.
Kiểu hình thức khung xương lại có thể phân làm hai loại:
- Kiểu nhánh khung xương.
- Kiểu tuyến mạng.
Kiểu hình thức mảng khối có thể phân làm hai loại:
- Kiểu khối đặc
- Kiểu khối rỗng
a) Kiểu nhánh khung xương
Là dạng kết cấu, cấu trúc được hợp bởi một số nhánh (tuyến) có chiều hướng khác nhau. Thường là lặp lại theo một quy luật nào đó. Các nhánh đều nối với trục (tuyến) chính thông qua các khớp nối. Ví dụ nhánh cây, cuống lá, bộ khung xương động vật.
Hình 7.15 là hình chụp hình ảnh bộ khung xương của thế giới sinh vật và hình ảnh ứng dụng kiểu nhánh khung xương trong xây dựng - kiến trúc.

Hình 7.15: Hình thức cấu kết nhánh khung xương
a. Thân cây - nhánh cây - cành cây.
b. Bộ xương khủng long với xương sống là tuyến chính, xương sườn, xương chân là nhánh phụ.
c. Bộ xương con ếch: nhánh chính là xương sống, xương ống chân, nhánh phụ là các xương bàn chân.
d. Bộ xương cá voi, tuyến chính là xương sống, tuyến phụ, tuyến nhánh là xương sườn và vây bơi.
e. The World Trade Center Transportation Hub. New York. 2014. Santiago Calatrava. Mái của nhà ga xe điện nhầm có kết cấu dạng nhánh khung xương. Hệ tuyến nhánh được tổ hợp theo kiểu lặp lại tiệm tiến, hình dạng đơn vị khung không thay đổi, kích cỡ thay đổi dần.
b) Kiểu tuyến mạng: Là dạng kết cấu, cấu trúc được tập hợp bởi các tuyến. Nhưng khác với hệ cấu tạo nhánh khung xương, các tuyến kiểu này được nối thông mạch nhau. Không có hoặc rất ít tuyến cụt, chúng nối kết với nhau thành mạng.
Hệ mạng này có thể là mạng phẳng, mạng cong hay mạng không gian ba chiều dày đặc.
Modun hệ lưới mạng có thể là tam giác, tứ giác, lục giác hay hệ đa lặp (ví dụ, kết hợp giữa tam giác và tứ giác).
Hình 7.16 là hình ảnh cấu tạo dạng tuyến mạng của thế giới sinh vật và một số công trình kiến trúc có kết cấu kiểu mạng.

Hình 7.16: Cấu tạo kiểu tuyến mạng
a. Gân lá cây kiểu mạng phẳng.
b. Mạng ba chiều của xơ mướp.
c. Mạng nhện kiều đồng tâm.
d. Mạng phẳng, tứ giác của các con ve sầu.
e. Mạng phẳng tứ giác và tam giác của cánh con chuồn chuồn.
f. Hình ảnh phóng to cấu trúc mạng ba chiều của xương động vật.
g. BMW Welt, Munich. 2006. Coop Himmelb(I)au. Hệ mạng không gian ô lưới tam giác, tứ giác được chuyển dạng kiểu xoay tỏa tạo nên diện mái, trần và tường cho nhà trưng bầy.
h. Milan, Trade Fair, Italy. 2004. Studio Fuksas. Mạng phẳng ba chiều ô lưới tam giác và tứ giác. Mặt phẳng mạng chuyển dần từ diện đứng sang diện ngang.
c) Kiểu mạng khối: Dạng thức này đối lập với hình thể có kết cấu khung xương hay tuyến mạng. Chúng không có nhánh, chúng có kết cấu thành từng cục, từng mảng; có thể là khối đơn lẻ hay kết nhóm lại với nhau.
Cảm nhận về khối thường là “ đặc chắc”, có trạng thái tĩnh, không động. Chúng mang vẻ đầy đặn và có cảm giác về trọng lượng. Tuy vậy, khối có thể có vai trò kép, tức vừa chiếm chỗ trong một khoảng không vừa có thể bị “rỗng ruột” tạo ra cái hốc trong nó. Ví như hòn đá cuội đặc chắc lại có lỗ thủng hay vỏ một con ốc.
Như vậy có hai loại khối: khối đặc và khối rỗng với từng cấp độ rỗng nhiều hay ít. Khối rỗng có thể tiến tới dạng kết cấu vách ví như vỏ ốc.
Với thế giới tự nhiên, những hình thể dạng khối thì không có khung xương (tuy vậy nếu phóng to nhiều lần lát cắt của xương động vật, ta lại có thể thấy cấu trúc kiểu mạng). Mặt khác, dạng khung xương lại có thể mang vẻ của dạng khối nếu khung xương có kích thước lớn (ví dụ một thân cây, cành cây to).
Với lí thuyết “quá trình giải khối” trong nghệ thuật tạo hình như điêu khắc, kiến trúc thì quan niệm về khối trong nghệ thuật khác với tự nhiên. Sự xuất hiên khối “âm”, khối “rỗng”, khối “thủng”, khối “ước lệ” để tương ứng với mục đích sử dụng, với ý đồ tác phẩm là thực tế và nhiều khi không có sự phân biệt giữa hai dạng khung xương - khung mạng với khối đặc - khối rỗng.
>>> Cách tạo hình trong vẽ cổ trang