Các dạng hình thể không gian (Phần 2)
2. Khối đa diện đều và bán đều:
Các khối cơ bản (Primary Solids), các khối đa diện đều và bán đều (Polyhedra) đã được biết từ thời Cổ đại: Pitago (Pythagore), Oclit (Euclid), Platon, Herong (Heron), Acsimet (Archimedes) đều đã biết. Thế kỉ XVII Johan Keple (Johannes Kepler) đã thiết lập được các quan hệ kích thước của chúng. Đến Louis Poinsot (1777 - 1859) và Ole (Euler 1707 - 1783) nghiên cứu về các đa diện này đã hoàn chỉnh.
Vẻ đẹp tạo hình của các khối này biểu hiện ở tính logic của cấu trúc và biến hóa về hình dạng. Do cạnh của các khối đa diện đều và bán đều là bằng nhau nên tổ hợp được cấu kết dế dàng.
Các tổ hợp khối đa diện đều và bán đều có thể phát triển theo kiểu lặp lại, kiểu tuyến tính, kiểu phân nhánh, kiểu mạng đa chiều,... Các khối có thể được xử lí kiểu khối đặc, khối rỗng, nửa đặc nửa rỗng, khối khấu trừ, khối trong suốt...
Khối đa diện đều
Khối đa diện đều (hay còn gọi là khối platon: Platonic Solids), là khối có các cạnh bằng nhau; các mặt cơ sở có kích thước và hình dáng giống nhau; các mắt (đỉnh) của khối là giống nhau.
Khối đa diện đều có sức lôi cuốn hấp dẫn nhưng đơn giản, được coi như cấu trúc cơ sở tạo nên mạng không gian hai hay ba chiều nghiêm ngặt và biến hóa.
Có 5 khối duy nhất: khối tứ diện (4 mặt tam giác), khối lập phương (6 mặt từ giác); khối bát diện (8 mặt tam giác); khối thập nhị diện (12 mặt ngũ giác) và khối nhị thập diện (20 mặt tam giác) (hình 7.42: hình vẽ lại sách: Morphogenese - Jean Marie delarue. 1983).
1. Khối tứ diện (Tetrahedron) (hình 7.42a)
- Có 4 mặt, 6 cạnh và 4 đỉnh.
- Mỗi mặt là tam giác đều.
- Nếu nhìn thẳng vào một mặt thì hình chiếu của khối sẽ tạo thành tam giác đều.
- Nếu nhìn thẳng vào một cạnh,hình chiếu khối có dạng hình vuông.
- Khối tứ diện là hình khối đơn giản nhất trong các khối platon. Nó là hình khối có cấu trúc ổn định, bền vững nhất mà con người có thể tạo ra.
2. Khối lập phương (Cube - Hexahedron) (hình 7.42b)
- Là khối dễ nhận biết và tĩnh tại nhất trong các khối platon (đã đề cập ở phần trên).
- Khối lập phương có 6 mặt hình vuông, 8 đỉnh và 12 cạnh.
- Nếu nhìn trực diện từ một mặt, hình chiếu sẽ là hình vuông.
- Nếu nhìn trực diện từ một đỉnh, hình chiếu của khối là hình lục giác.
3. (Octahedron) (hình 7.42c)
- Là khối kép (khối dối ngẫu) của khối lập phương. Có nghĩa khối đa diện 8 mặt được tạo thành nếu thay đổi số đỉnh của khối lập phương bằng số mặt của khối đa diện 8 mặt và thay số mặt của khối lập phương bằng số đỉnh của khối đa diện 8 mặt.
- Khối có 8 mặt, 6 đỉnh, 12 cạnh.
- Nếu nhìn từ đỉnh thì hình chiếu là hình vuông.
- Nếu nhìn thẳng từ một góc mặt thì hình chiếu bằng của khối là một hình lục giác đều.
4. Khối thập nhị diện (Đoecahedron) (hình 7.42d)
- Được tham khảo từ các hình ngũ giác đều.
- Có 12 mặt, 20 đỉnh, 30 cạnh.
- Nhìn trực diện từ một mặt, hình chiếu của khối là hình thập giác (10 cạnh).
5. Khối nhị thập diện (Icosahedron) (hình 7.42e)
- Được tham khảo từ các hình tam giác.
- Có 20 mặt tam giác, 12 đỉnh, 30 cạnh.
- Là khối đối ngẫu của khối thập nhị diện.

Hình 7.42: Các khối đa diện đều. Hình vẽ thể hiện phối cảnh các khối đa diện đều và hình đối ngẫu của nó. Phần dưới là khai triển các diện tham tạo khối trên mặt phẳng và các hình chiếu ở một số vị trí đặc biệt.
a. Khối tứ diện (khối 3.3.3).
b. Khối lập phương (khối 4.4.4).
c. Khối bát diện (khối 3.3.3.3).
d. Khối thập nhị diện (khối 5.5.5).
e. Khói nhị thập diện (khối 3.3.3.3.3).
Khối đa diện bán đều
Khối đa diện bán đều (hay còn gọi là khối Arsimet - Archimedean Solids) là khối có các cạnh bằng nhau, các mặt của khối tại một đỉnh lớn hơn hai loại mặt đa giác đều.
- Khối đa diện bán đều được hình thành từ sự cắt cụt các đỉnh của các đa diện đều. Việc cắt các đỉnh phải tính toán độ nông, sâu để khối mới xuất hiện có các diện đa giác đều và các cạnh của chúng bằng nhau. Xem ví dụ hình 7.43, từ khối bát diện đều (tám mặt tam giác) cắt cụt các đỉnh có mức độ sẽ được khối đa diện bán đều có mặt tứ giác và lục giác (khối 4.6.6).
- Từ một khối gốc đa diện đều, nếu cắt sâu hay nông sẽ được các khối đa diện bán đều khác nhau. Ví dụ hình 7.44, với hình lập phương nếu cắt ở các đỉnh không sâu lắm sẽ được khối (3.8.8), nếu cho lát cắt sâu hơn lại được một khối đa diện bán đều khác khối (3.4.3.4).
- Có 13 khối đa diện bán đều, xem hình 7.45.
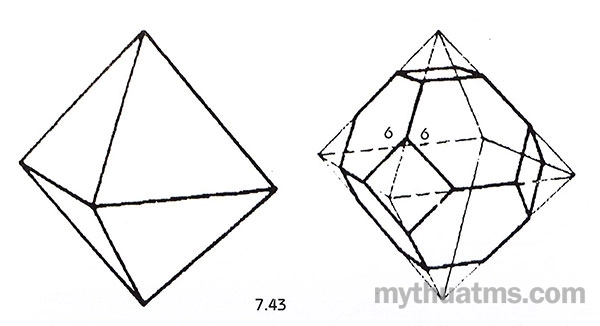
Hình 7.43: Cắt cụt khối các đỉnh của khối đa diện đều (khối đa diện platon) sẽ có khối đa diện bán đều (khối đa diện Archimed). Hình vẽ thể hiện việc cắt cụt các đỉnh khối bát diện vừa độ sẽ tạo ra khối đa diện bán đều có mặt lục giác và tứ giác.
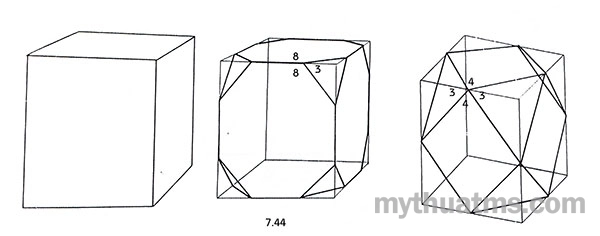
Hình 7.44: Nếu cắt đỉnh khối đa diện đều nông sâu khác nhau sẽ có các khối đa diện bán đều khác nhua. Hình lập phương, cắt các đỉnh với độ nông sâu khác nhau sẽ cho hai khối đa diện bán đều khác nhau là khối (3.8.8.) và (3.4.3.4).
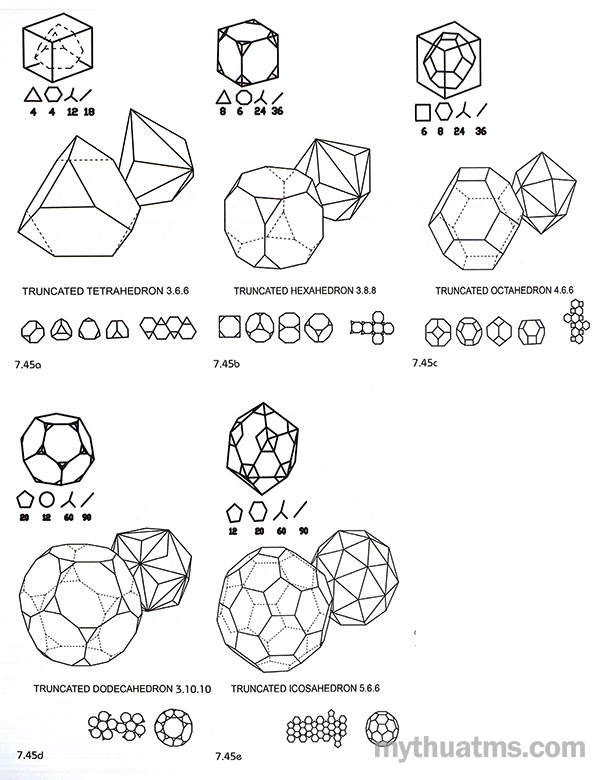
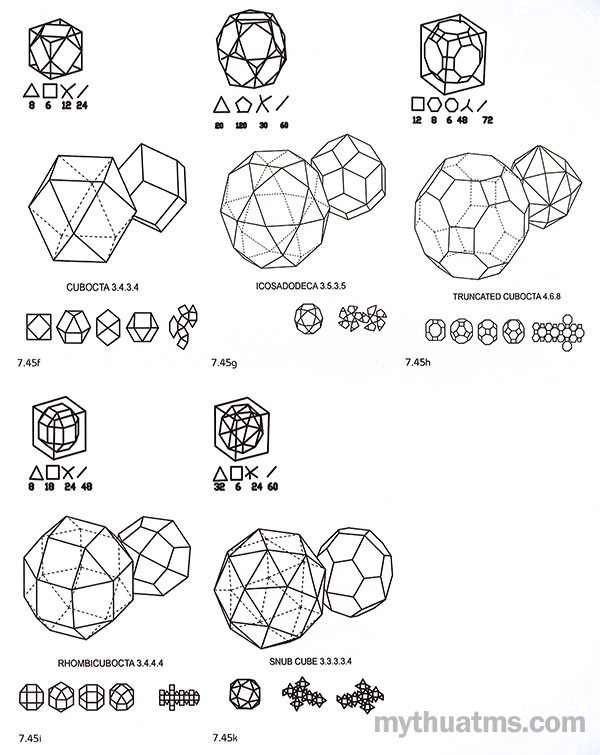
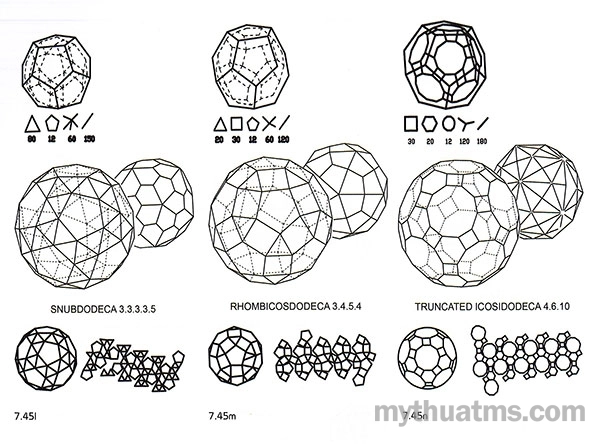
Hình 7.45: 13 khối đa diện bán đều
a. Tứ diện cụt - Truncated Tetrahedron - (3.6.6).
b. Lập phương cụt - Truncated Hexahedron - (3.8.8).
c. Bát diện cụt - Truncated Octahedron - (4.6.6).
d. Thập nhị diện cụt - Truncated Icosahedron - (5.10.1).
e. Nhị thập diện cụt - Truncated Icosahedron - (5.6.6).
f. Cubocta (3.4.3.4).
g. Icosadodeca - (3.5.3.5).
h. Cubocta cụt - Truncated Cubocta - (4.6.8).
i. Rhombicubota - (3.4.4.4)
k. Snub Cube (3.3.3.4).
l. Snubdodeca - (3.3.3.3.5).
m. Rhombicosdodeca (3.4.5.4).
n. Icosidodeca cụt - Trucated Icosidodeca - (4.6.10).
Cách gọi tên khối đa diện:
Để thuận tiện nhận dạng, cần gọi tân khối đa diện đều và bán đều. Có hai cách đánh mã số từng khối vào số cạnh của diện đa giác tham tạo nên khối là cách gọi theo đỉnh và theo mặt
a) Cách gọi tên theo đỉnh
- Ví dụ có khối (3.6.6).
Khối (3.6.6) là khối đa diện bán đều. Mỗi đỉnh của nó được tham tạo bởi 3 mặt (n=3). Mặt thứ nhất có 3 cạnh, mặt thứ hia có 6 cạnh và mặt thứ ba có 6 cạnh. Xem hình 7.45a.
b) Cách gọi tên theo mặt
Ví dụ có khối (3.5.3.5).
Đây là khối đa diện có các mặt giống nhau đều có 4 cạnh (n=4). Đỉnh thứ nhất của tứ giác có 3 cạnh gặp nhau, đỉnh thứ hai có 5 cạnh gặp nhau, đỉnh thứ ba có 3 cạnh gặp nhau, đỉnh thứ tư có 5 cạnh gặp nhau. Xem hình 7.45g.
Khối đối ngẫu
Một khối có hai cách gọi khác nhau. Hai khối khác nhau được hiểu từ một tên gọi, gọi là khối đối ngẫu (duality). Hình 7.42 và 7.45 là các hình vẽ khối đa diện đều, bán đều và khối đối ngẫu của nó.
Hình 7.46 là ví dụ ba khối platon có tâm điểm các mặt của đa diện biến thành các đỉnh của đa diện đối ngẫu, các đỉnh của đa diện đối xứng với các mặt đa diện đối ngẫu, còn số cạnh không thay đổi.

Hình 7.46: Các ví dụ về khối đối ngẫu của ba khối platon; mặt - thành đỉnh, đỉnh - thành diện; số cạnh không thay đổi (ảnh chụp lại sách: Shapes, Space and Symmerty - Alan Holden).
a. Khối tứ diện và khối đối ngẫu: khối tứ diện.
b. Khối lập phương và khối đối ngẫu: khối bát diện .
c. Khối thập nhị diện (mặt ngũ giác) và khối đối ngẫu: khối nhị thập diện (mặt tam giác).
Xử lí khối đa diện đều và bán đều
a) Xử lí diện
- Làm rỗng khối đa diện, tạo nên không gian bên trong khối bằng cách khoét bỏ phần lớn bề mặt diện hay chỉ để lại các bờ cạnh dưới dạng thanh. Hình 7.47a là ví dụ lấy khối bát diện minh họa.
- Mỗi mặt phẳng của đa diện được làm lồi ra hay lõm vào tạo nên khối âm, khối dương cho khối. Ở ví dụ hình 7.47b, phần lồi, lõm này được kiến tạo từ các mặt tam giác. Theo cách này hình dạng bề ngoài của khối đa diện có thể bị biến dạng thành khối đa diện hình sao.
- Có thể kết hợp những khối nhỏ độc lập với các mặt của đa diện (hình 7.47c).
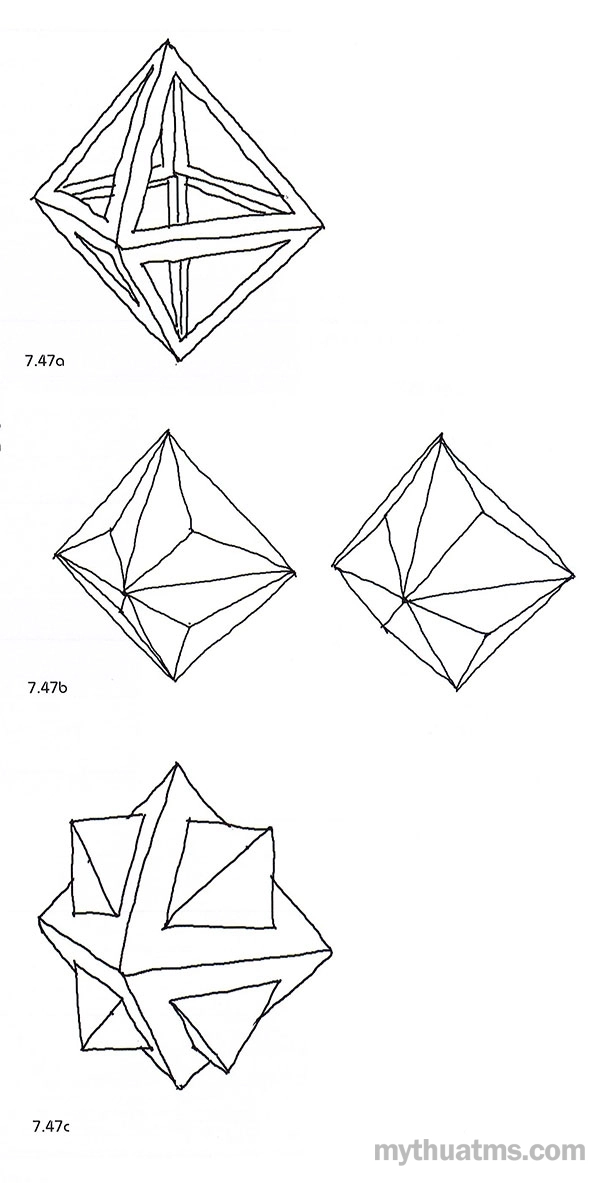
Hình 7.47: Xử lí diện khối đa diện.
a. Khoét bỏ một phần bề mặt diện.
b. Làm lồi hay lõm vào mặt đa diện.
c. Thêm khối độc lập vào bề mặt khối đa diện.
b) Xử lí cạnh
- Xử lí cạnh bằng cách cộng thêm khối, trừ đi khối theo các cạnh của khối đa diện. Khi trừ đi một phần của cạnh là đã trừ đi một phần của diện dẫn tới bớt đi khối (hình 7.28a).
- Các cạnh của khối đa diện có thể xử lí làm cong đi hoặc gẫy khúc, điều này sẽ làm cho khối phồng lên hoặc thêm nhiều diện (hình 7.48b).
- Thay thế cạnh đơn bằng cạnh kép (hình 7.48c).
- Cài lồng các mặt theo nhiều cách khác nhau dọc theo cạnh của khối đa diện (hình 7.48d).
c) Xử lí các đỉnh
- Có thể cắt cụt đỉnh của khối, như vậy sẽ tạo nên một mặt mới tại vị trí cắt đỉnh, đồng thời một khối mới hình thành (hình 7.49a).
- Việc xử lí đỉnh bằng cách thêm khối vào vị trí đỉnh (hình 7.49b).
d) Kết hợp các khối đa diện
- Các khối đa diện có thể kết hợp với nhau theo cách: các khối tiếp xúc qua diện, các khối tiếp xúc qua cạnh, các khối đấu đỉnh với nhau (hình 7.50a).
- Các khối đa diện có thể cài lồng vào nhau (hình 7.50b).
- Kiểu khối nằm trong khối dạng đối ngẫu, hay khối trong khối kiểu đồng dạng, dạng nghịch đảo, dạng xoay trượt, kiểu tự do...
Xem hình 7.50c.
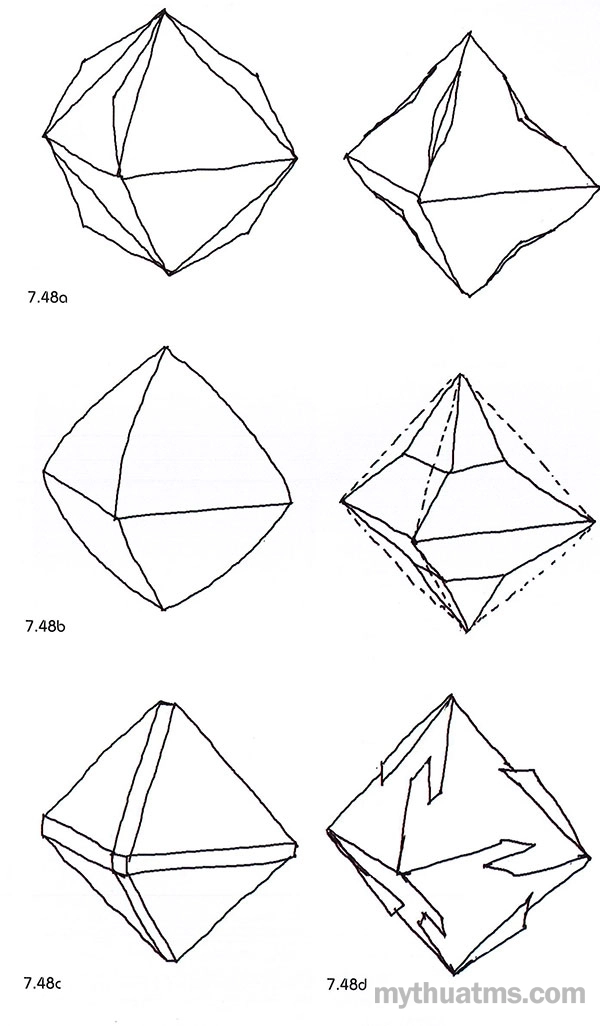
Hình 7.48: Xử lí cạnh khối đa diện
a. Cộng hay bớt đi cạnh khối đa diện.
b. Làm cong hay gẫy khúc cạnh khối đa diện.
c. Thay thế cạnh đơn bằng cạnh kép.
d. Cài lồng hai mặt liền kề nhau của khối đa diện để phá bỏ cạnh gốc của khối.
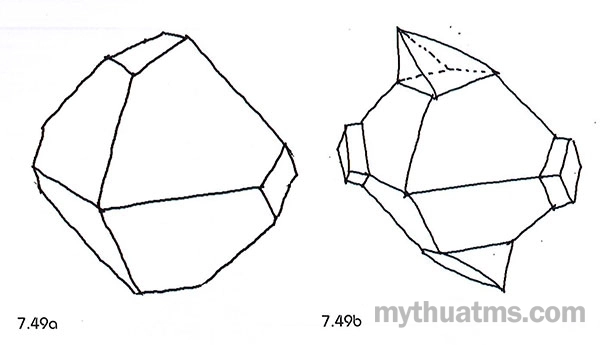
Hình 7.49: Xử lí đỉnh khối đa diện
a. Cắt cụt đỉnh khối đa diện.
b. Thêm khối mới vào đỉnh khối đa diện.
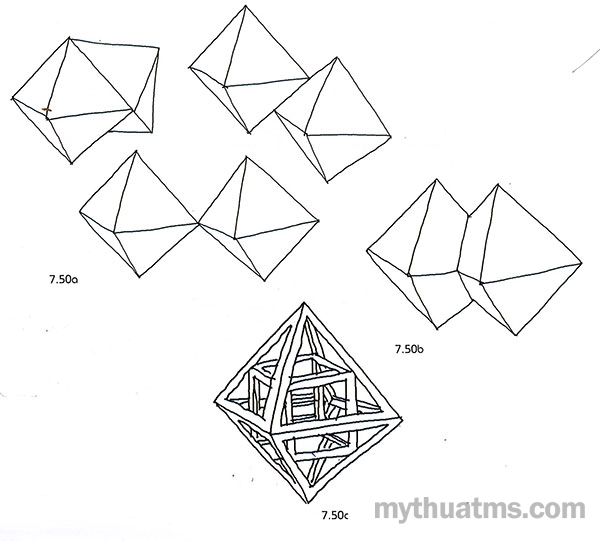
Hình 7.50: Kết hợp các khối đa diện
a. Tiếp xúc các khối thông qua diện - cạnh - đỉnh.
b. Các khối đa diện gioa thoa nhau, cài lồng vào nhau.
c. Kiểu khối trong khối.
e) Kết luận: Trên đây là một số thủ pháp xử lí có tính chất đặc trưng cho khối đa diện đều và bán đều. Việc xử lí nhằm phá bỏ thể đối xứng tạo thêm vẻ phong phú về tạo hình cho loại khối này. Có thể tham khảo thêm phần trước “Xử lí khối cơ bản”. Cụ thể ở các thủ pháp:
a. Khấu trừ khối.
b. Cắt vát khối.
c. Chia cắt khối và dịch chuyển.
d. Khối cộng thêm.
BÀI THỰC HÀNH 7.2: Tạo hình khối đa diện đều và bán đều
Chọn từ 1 - 3 khối đa diện đều và bán đều (trong 18 khối) để làm nên một tác phẩm tạo hình. Có thể dùng các thủ pháp: khấu trừ khối, cắt vát khối, chia cắt khối, cộng thêm khối thông qua xử lí diện, cạnh, đỉnh. Xem các ví dụ hình 7.51 (Bài tập này có thể chia tách làm nhiều bài tập nhỏ với các thủ pháp khác nhau).
Hình 7.51: Tạo hình với khối đa diện đều và bán đều

Hình 7.51a: Một khối đa diện bán đều (3.4.4.4) được trừ đi một số mặt tam giác và tứ giác, khối được rỗng đi một phần, lộ ra 6 khối hộp bên trong. ( Bài tập sinh viên).
Hình 7.51b: Ba khối đa diện bán đều (3.4.3.4) nội tiếp nhau. Các khối được sắp xếp đảo chiều. Một dạng khối trong khối bố trí cân đối. (Bài tập sinh viên).
Hình 7.51c: Khối đa diện bán đều (3.4.3.4) được làm rỗng. Tại các diện tam giác khối được cộng thêm các khối phụ tứ diện đều (3.3.3). Khối chung mang dáng vẻ gai góc. (Bài tập sinh viên).
Hình 7.51d: Một số đa diện bán đều được làm lõm vào, phần lõm được kiến tạo từ các mặt tam giác. (Bài tập sinh viên).
Hình 7.51e: Một khối đa diện bán đều (3.4.3.4) có các bề mặt được khoét rỗng một phần. Diện tứ giác được làm lõm vào trong. (Bào tập sinh viên)
Hình 7.51f: Khối đa diện đều (3.3.3.3.3) có các cạnh được làm cong lõm. Hai khối cài lồng vào nhau, tạo nên cấu trúc dạng mạng ba chiều. (Bài tập sinh viên).
Hình 7.51g: Một khối đa diện đều được cộng thêm các khối tứ diện. (Bài tập sinh viên).
Hình 7.51h: Một khối đa diện đều có các mặt được xử lí bong ra ngoài và uốn cong (ảnh chụp từ sách Principles of form and Design - Wucius Wong).

Hình 7.51i: Một khối đa diện đều có cạnh của khối được xử lí thành cạnh kép. Đỉnh của khối biến đổi thành diện hình ngôi sao tám cánh (ảnh chụp từ sách: Spapes, Space, and Symmerty - Alan Holden).
Hình 7.51k: Hợp nhóm khối đa diện đều tứ diện (3.3.3) theo cách diện tiếp xúc diện trùng khít. Tổ hợp kiểu dạng tập theo tuyến xoáy tròn. Hợp nhóm khối kết hợp với hệ thanh đã cho tổ hợp vẻ thanh thoát uyển chuyển. (Bài tập sinh viên).
Hình 7.51l: Ba khối bát diện rỗng nội tiếp trong nhau và đồng dạng. Các thanh của khối được phân thành mạng tam giác, đấu kết với nhau. Hợp nhóm mang tính tầng bậc và đa chiều. (Bài tập sinh viên)
Hình 7.51m: Ba khối tứ diện rỗng giao thoa - cài lồng nhau. (Bài tập sinh viên).
Hình 7.51n: Kết hợp các khối đa diện bán đều (3.6.6) theo cách tiếp xúc diện và đấu đỉnh cấu trúc kiểu phân nhánh. Một số khối được chuyển dạng theo kiểu cộng thêm, tạo sự đa dạng về khối hình cho tổ hợp. (Bài tập sinh viên)
Hình 7.51p: Hợp nhóm các khối tứ diện kiểu tiếp xúc đỉnh, tiếp xúc cạnh tổ hợp theo tuyến cong. (Bài tập sinh viên).
Hình 7.51q: Khối đặc kết hợp với khối rỗng, hay mạng kết hợp với khối đặc. Phần mạng có gốc là khối (3.3.3), các cạnh được biến chuyển về kích cỡ và chiều hướng. Hợp nhóm được tổ chức dạng tập trung quanh điểm. (Bài tập sinh viên).
Hình 7.51r: Ba khối (4.6.6) nội tiếp trong nhau. Bố cục kiểu đảo chiều, đối xứng qua tâm. (Bài tập sinh viên)

Hình 7.51s: Bày khối (3.8.8) nội tiếp trong nhau. Bố cục đối xứng qua trục, sắp xếp kiểu đồng dạng. (Bài tập sinh viên).
Hình 7.51t: Các khối (3.3.3) cài lồng vào nhau tạo ra nhịp điệu tiện tiến. Hợp nhóm theo tuyến cong. (Bài tập sinh viên)
Hình 7.51u: Kết hợp qua khối đa diện đều (3.3.3.3.3), khối (3.5.5) theo kiểu khối trong khối. Bố cục kiểu đối xứng qua tâm. (Bài tập sinh viên).
Hình 7.51x: Ba biến thể của khối đa diện đều theo cách xử lí diện bằng cách cộng thêm khối hình sao, biến đổi cạnh bằng cách tạo diện, kéo dài và chuyển dạng diện cơ sở. (Bài tập sinh viên)
Hình 7.51y: Hợp nhóm khối lập phương, khối (3.3.3.3.3) khối tứ diện (3.3.3) và hệ mạng ba chiều tam giác. Bố cục kiểu tầng bậc, đặc rỗng. Tổ chức theo kiểu tập trung quanh một trục. (Bài tập sinh viên).
3. Khối lăng trụ - nghịch lăng trụ và khối trụ:
a. Hình lăng trụ:
Khối hình lăng trụ là các khối có các cạnh đáy bằng nhau và đồng dạng.
- Khi các bờ cạnh bên vuông góc với đáy gọi là lăng trụ thẳng (Right Prism) (hình 7.52a).
- Khi các bờ cạnh bên không vuông góc với đáy cơ sở gọi là lăng trụ xiên (Oblique Prism) (hình 7.52b).
- Khi các đa giác cơ sở là các đa giác đều gọi là lăng trụ đều (Regular Prism) (hình 7.52c).
Tên lăng trụ phụ thuộc vào hình dạng của đa giác cơ sở (đa giác gốc). Ví dụ hình cơ sở là tam giác, có lăng trụ tam giác; nếu đa giác gốc là hình ngũ giác, có lăng trụ ngũ giác.
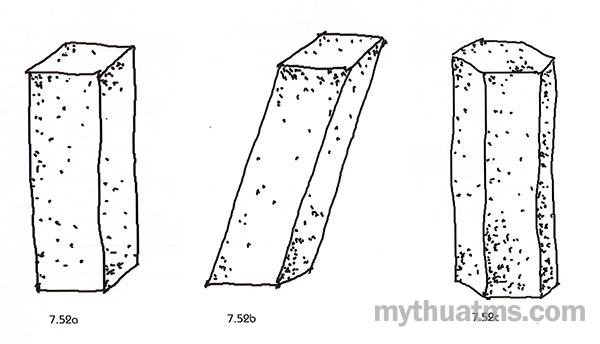
Hình 7.52: Hình lăng trụ
a. Lăng trụ thẳng.
b. Lăng trụ xiên.
c. Lăng trụ đều lục giác.
* Hình lăng trụ và khả năng biến đổi của nó:
- Hai đáy có thể là các dạng đa giác bất kì, hình tam giác, hình vuông, ngũ giác (hình 7.53a).
- Các cạnh bên lăng trụ không nhất thiết phải song song với nhau (hình 7.53b).
- Hai đa giác cơ sở có thể không song song với nhau (hình 7.53c).
- Hai đáy không nhất thiết phải cùng hình dáng và kích thước (hình 7.53d).
- Các cạnh của lăng trụ có thể là đường cong, đường gấp khúc, đường zic-zắc… khi đó thiết diện ở mỗi đoạn lăng trụ có kích thước khác nhau, hình dạng khác nhau (hình 7.53e).
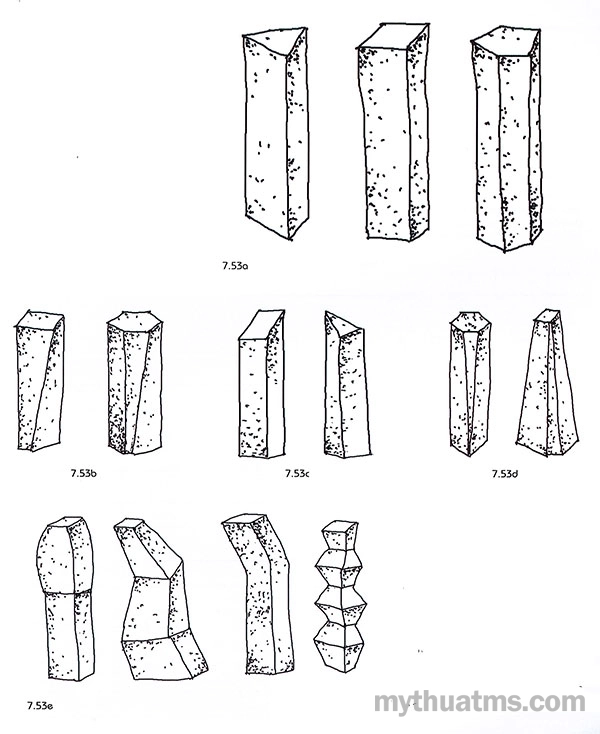
Hình 7.53: Hình lăng trụ và khả năng biến đổi
a. Các đáy là các loại dạng đa giác khác nhau.
b. Các cạnh bên lăng trụ không nhất thiết phải song song với nhau.
c. Hai đáy cơ sở không song song với nhau.
d. Hai đáy cơ sở có thể không cùng kích cỡ hình dạng.
e. Các cạnh bên của khối lăng trụ có thể là cong hoặc thẳng, là zic-zắc, cong đều…
b/ Khối hình nghịch lăng trụ: Khối hình nghịch lăng trụ (antiprism) có các tính chất sau:
- Các đáy là đa giác đều, đáy trên, đáy dưới lệch nhau;
- Các mặt bên là các tam giác đều tham tạo nên khối nghịch lăng trụ.
Muốn tạo nên nghịch lăng trụ chỉ cần xoay đáy trên của lăng trụ quanh trụ đứng trung tâm một góc nào đó rồi nối các đỉnh của đáy trên và dưới với nhau.
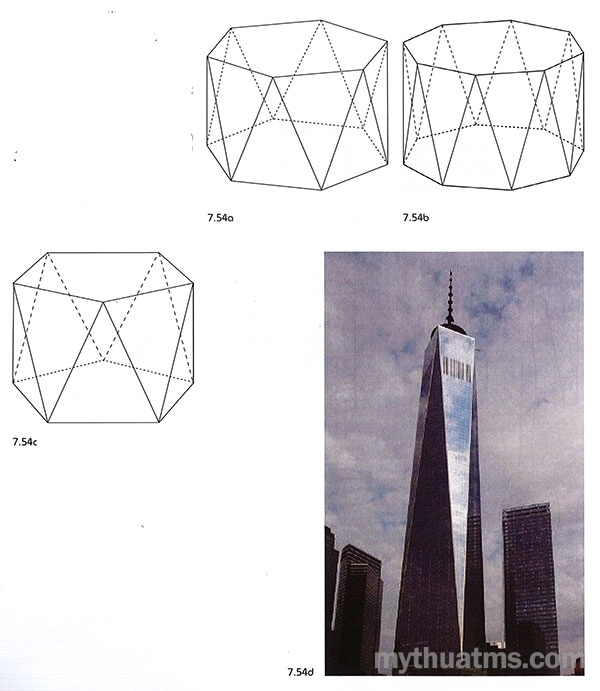
Hình 7.54 là các khối nghịch lăng trụ đều lục giác, bát giác đều, ngũ giác đều và công trình Trung tâm thương mại Thế giới (tòa nhà số ) có hình khối dạng nghịch lăng trụ.
Hình 7.54: khối hình nghịch lăng trụ
a. Nghịch lăng trụ đều lục giác.
b. Nghịch lăng trụ đều bát giác.
c. Nghịch lăng trụ đều ngũ giác.
d. Trung tâm thương mại Thế giới – New York – tòa nhà số 1. 2014. SOM. Một dạng nghịch lăng trụ, có đáy trên đáy dưới là hình vuông nhưng khác nhau về kích cỡ và xoay lệch nhau 45 độ.
c/ Khối hình trụ: Hình trụ chuẩn bao gồm hai đáy là hình tròn song song có cùng kích cỡ, thân vuông góc với đáy. Từ hình trụ chuẩn có các biến thể của hình trụ như sau:
- Thân nghiêng, không vuông góc với đáy (hình 7.55a).
- Hai đáy là các hình có các cạnh thẳng nhưng góc nguýt tròn (hình 7.55b).
- Hai đáy có thể khác nhau về hình dạng và kích cỡ (hình 7.55c).
- Thân có thể cong đều (hình 7.55d).
- Thân có thể gấp khúc (hình 7.55e).
- Thân có thể gấp khúc chỗ to, chỗ nhỏ (hình 7.55f).
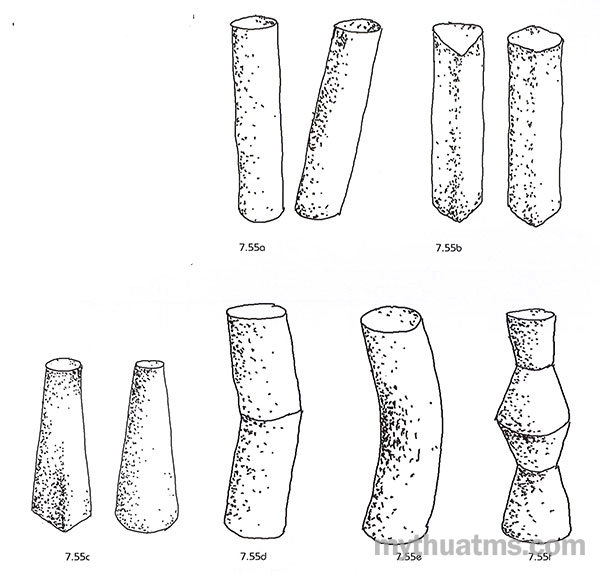
Hình 7.55: Biến thể khối trụ
a. Thân nghiêng.
b. Hai đáy là đa giác góc tròn.
c. Hai đáy có thể khác nhau về kích cỡ và hình dạng.
d. Thân gấp khúc.
e. Thân cong.
f. Thân to nhỏ khác nhau.
Xử lí khối lăng trụ:
a) Xử lí bề mặt đỉnh (đáy) lăng trụ:
- Đáy có thể rỗng, đậy kín hoặc có khoét thủng (hình 7.56a).
- Đáy hay đỉnh có thể chia làm nhiều phần (hình 7.56b).
- Đáy hay đỉnh có thể chia cắt lại các diện, thay đổi dạng kết cấu (hình 7.56c).
- Có thể chồng xếp, cộng them các khối vào đỉnh hoặc đáy (hình 7.56d).
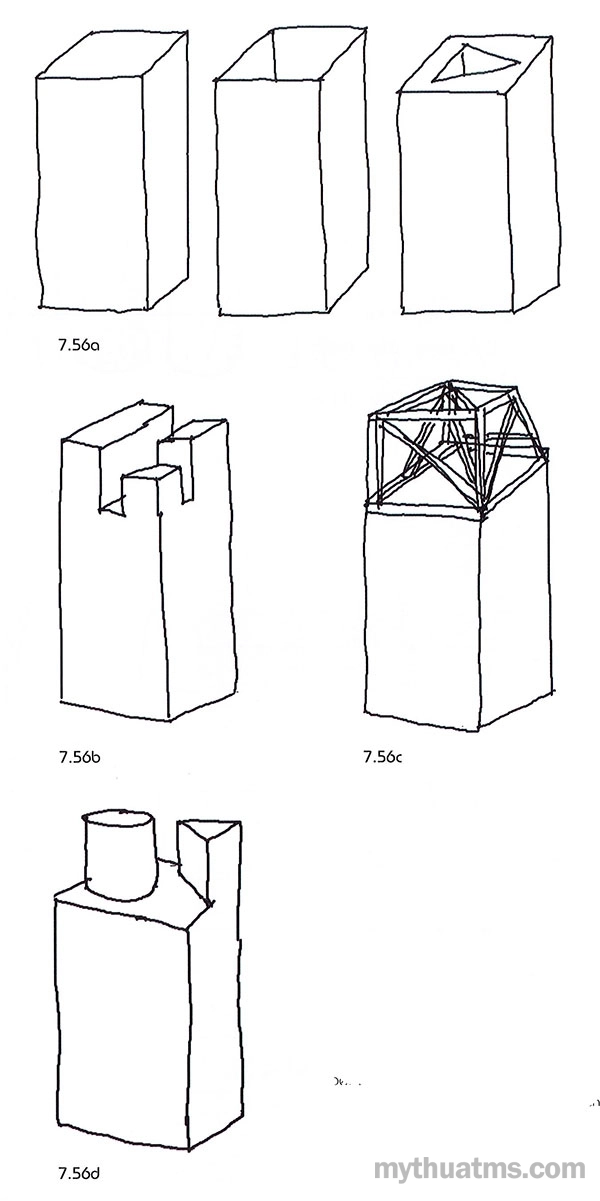
Hình 7.56: Xử lí đỉnh hoặc đáy lăng trụ
a. Đáy có thể đậy kín, làm rỗng, hoặc khoét diện.
b. Đáy (đỉnh) được chia làm nhiều phần.
c. Đáy có thể thay đổi dạng kết cấu, hình thể.
d. Cộng thêm khối mới vào đáy.
* Xử lí bờ cạnh khối lăng trụ:
- Tạo các cạnh đứng không song song (hình 7.57a).
- Tạo các cạnh đứng cong lượn sóng (hình 7.57b).
- Cắt bỏ bớt bờ cạnh làm thay đổi hình dạng diện đứng (hình 7.57c).
- Tạo các bờ cạnh giao nhau (dạng nghịch lăng trụ) (hình 7.57d).
* Xử lí diện khối lăng trụ:
- Có thể cắt bỏ một phần bề mặt diện (hình 7.58a).
- Tạo lỗ trên bề mặt đứng. Miếng cắt có thể bẻ ra ngoài hay ấn vào trong (hình 7.58b).
- Gắn thêm khối vào bề mặt diện (hình 7.58c).
* Kết luận: Khối lăng trụ, nghịch lăng trụ và khối trụ là các dạng khối hay được sử dụng trong tạo hình, đặc biệt là kiến trúc bởi hình thức phong phú, khuôn hình dài nên có thể chứa đựng nhiều không gian chức năng bên trong nó. Các khối này có thể dựng đứng hay nằm ngang.
Việc xử lí cần tham khảo thêm ở phần trước , khối cơ bản bởi hai chủng loại khối này có nhiều đặc điểm tương đồng. Cụ thể các thủ pháp này là:
a – Khấu trừ khối
b – Cắt vát khối kiểu trực diện hay vát cạnh.
c – Chia cắt khối và dịch chuyển theo kiểu xoay trượt, tịnh tiến… và mở rộng khe chia cắt.
d – Cộng thêm khối, phát triển khối theo kiểu khối độc lập hay khối có các cạnh cơ bản trùng nhau…
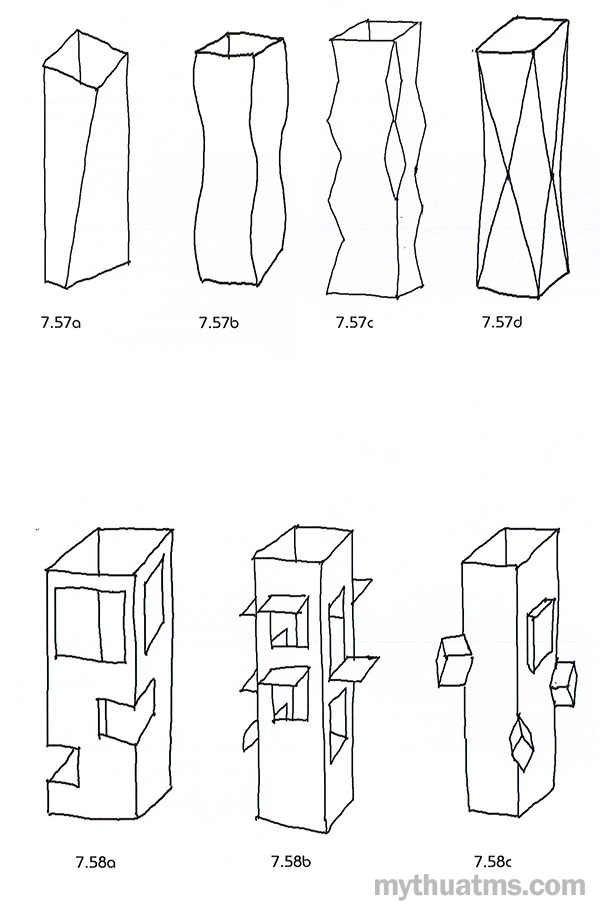
Hình 7.57: Xử lí bờ cạnh khối lăng trụ
a. Tạo các cạnh đứng không song song.
b. Tạo các cạnh đứng lượn sóng.
c. Bỏ bớt, ngắt quãng các bờ cạnh.
d. Tạo các bờ cạnh giao nhau.
Hình 7.58: Xử lí diện khối lăng trụ
a. Cắt bỏ, đục, khoét một phần diện theo các cấp độ, dạng hoa văn khác nhau.
b. Tạo lỗ trên bề mặt. Miếng cắt có thể được uốn vào trong hay đẩy ra ngoài.
c. Thêm vào bề mặt diện một khối độc lập.