Nguyên tắc tổ hợp (Phần 2)
5. Nhịp điệu: Trong tự nhiên rất nhiều hiện tượng, sự việc được lặp lại và tạo ra nhịp điệu hay còn gọi là vần luật. Ví dụ, hoạt động của con người đi đứng, chạy nhảy, bơi lội, khiêu vũ, nện búa,... đều cần đến sự chừng mực - nhịp điệu. Các hoạt động cũng như các hiện tượng tự nhiên khác đã được con người cách điệu hóa, mô phỏng đưa vào nhiều loại hình nghệ thuật như thi ca, âm nhạc, vũ đạo, chế tác đồ trang sức, quần áo, tranh vẽ, kiến trúc... theo vần luật - nhịp điệu rất đa dạng.
Tính nhịp điệu trong nghệ thuật thường xuất phát từ sự lặp lại của một hay một vài yếu tố nào đó theo quy luật, một chu kì nhằm mang lại vẻ hài hòa và sự cuốn hút cho hành động, cho tác phẩm. Cụ thể với nghệ thuật tạo hình đó là sự lặp lại có nhịp điệu các yếu tố thị giác như: nét, hình dạng, màu sắc, vị trí, chiều hướng hoặc một hình thái cấu trúc theo quy luật nào đó. Sự lặp lại những yếu tố này cần có số lượng lớn hơn ba (hơn ba phần lặp lại) để tạo ra hiệu ứng nhịp điệu.
* Các hình thức nhịp điệu: Các hình thức nhịp điệu được phân loại sau đây chỉ xét dưới dạng hình thức cấu trúc của tổng thể tổ hợp.
a) Nhịp đều liên tục: Là sự lặp lại y nguyên, liên tục của một hay một số yếu tố tạo hình. Nếu lặp lại chỉ một yếu tố, hay chỉ một nhóm chi tiết đặt cạnh nhau liên tục ta có nhịp đều liên tục đơn (xem hình 4.25a). Nếu lặp lại với một hay một số yếu tố và lặp lại một cách thuần tự theo quy luật nào đó, ta có nhịp đều liên tục phức hợp (xem hình 4.25b,c).
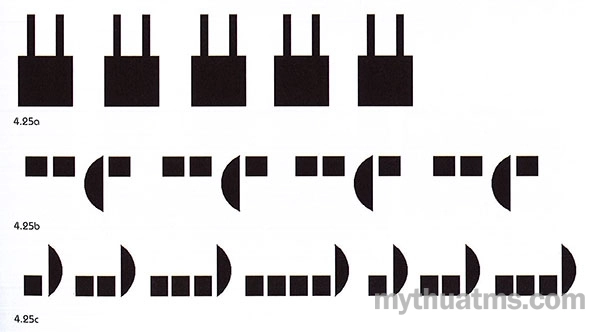
Hình 4.25: Nhịp đều liên tục
a. Hình vuông và hai dấu gạch thẳng đứng được lặp lại hơn ba lần, với khoảng cách đều đặn và y hệt nhau đã tạo ra nhịp điệu liên tục đơn.
b. Lặp lại yếu tố kép: hình vuông - hình vuông và hình viên phân. Hình vuông được lặp lại đều đặn, tạo ra nhịp đều liên tục phức hợp.
c. Nhịp lặp lại tăng dần - phức hợp. Số lượng hình vuông tăng dần và lặp lại sau bốn nhịp.
b. Nhịp tiệm tiến (progressive rhythm): Là sự lặp lại một hay một số yếu tố nào đó, nhưng các yếu tố này được biến đổi, chuyển dạng dần dần theo một hay vài quy luật nào đó. Hình thái này xuất hiện nhiều trong giới tự nhiên, ví dụ cách tổ chức lông cánh của một con chim (hình 4.26a). Hình 4.26b là ví dụ về nhịp điệu tiệm tiến mà đơn vị lặp lại có sự thay đổi về kích cỡ nhưng không thay đổi về hình dạng. Hình 4.26c là bài tập của sinh viên về biến điệu một hình tam giác, thao tác đã tạo ra nhịp điệu dạng tiệm tiến trong không gian 3 chiều.
Trong kiến trúc, thủ pháp lặp lại một tuyến, một hình dạng diện, một hình dạng khối hay một khối hình thái cấu trúc nào đó có biến đổi và chuyển dạng dần để tạo ra nhịp tiệm tiến rất hay được sử dụng. Cách thức tạo hình này dễ đạt được tính hài hòa thống nhất cho hình thức đồng thời mang lại logic về cấu trúc - kết cấu cho công trình. Hình 4.26d là ví dụ về cách xử lí hệ che chắn cho hành lang bên của một nhà thờ.

Hình 4.26: Nhịp tiệm tiến
a. Cấu trúc cánh con chim. Các lông cánh được sắp xếp kiểu tập trung theo tuyến, nhịp lặp lại kiểu tiệm tiến.
b. Các hình viên phân được lặp lại hình dạng, kích thước của hình đơn vị thay đổi tạo ra nhịp tiệm tiến.
c. Khung của khối đa diện tam giác đều, chuyển dịch trong không gian 3 chiều theo dạng quỹ đạo cong. Kích thước khối biến đổi kiểu tiệm tiến thu nhỏ dần. Đây là nhịp tiệm tiến kép trong không gian 3 chiều. (Bài tập sinh viên).
d. Greg Lynn Form. Korea Presbyteriar Church. New York. USA. 1999. Tấm che chắn hành lang bên khán phòng được tạo từ sự lặp lại có chuyển dạng của các diện đa giác. Các diện biến đổi dần tạo nên nhịp tiệm tiến thú vị, khúc chiết.
* Bài thực hành 4.3: Tạo nhịp tiệm tiến
Tạo nhịp tiệm tiến của một hình phẳng hoặc một hợp nhóm tuyến trong không gian ba chiều. Dùng phép biến đổi dần hình dạng, kích thước, chiều hướng hình cơ sở. Sự lặp lại hình thể bố trí theo tuyến thẳng tuyến cong, xoay tỏa... Xem ví dụ hình 4.27.

Hình 4.27: Tạo nhịp tiệm tiến trong không gian ba chiều ( bài tập sinh viên)
a. Các diện được lặp đi lặp lại theo kiểu tiệm tiến, hình dạng diện không đổi.
b. Các tuyến tạo thành nhịp mềm tiệm tiến cao dần.
c. Các thanh đứng xoay chuyển, các tuyến ngang trượt đều cao dần.
d. Khung tam giác xoay đều, nhỏ đều kiểu tiệm tiến kép.
c. Nhịp điệu dạng lượn sóng hay nhịp mềm: Các yếu tố tạo nhịp được lặp lại theo quy luật tăng, giảm đều, tạo nên hình thái chung là sự mềm mại, lượn sóng - lồi lõm hoặc có dao động hình sin.
Thông thường nếu các yếu tố thành phần là tuyến cong hoặc hình dạng cong, mềm mại thì hiệu quả tạo nhịp mềm càng rõ nét. Xem hình 4.28.
d. Nhịp điệu giao thoa (rhythm interlaced) được hình thành từ các hình dạng, tuyến, diện, hoặc khối đan chéo vào nhau theo một quy luật hay sơ đồ cấu trúc nào đó.
Nhịp điệu dạng giao thoa không giống các loại nhịp điệu khác là triển khai theo một hướng mà nó được đan chéo, cài lồng tạo hiệu quả đa hướng cho tổ hợp.

Hình 4.28: Nhịp mềm - nhịp lượn sóng
a. Đây là bài tập của sinh viên về sự lặp lại của một tập hợp diện. Các diện lặp lại không có sự thay đổi về hình dạng, kích thước, chiều hướng nhưng về vị trí có sự thay đổi theo một tuyến cong. Do vậy sự lặp lại đã tạo nên nhịp lượn sóng - nhịp mềm cho tổ hợp chung.
b. Liège - Guillemins TGV Railway Station. Liège, Belgium, 2009. Santiago Calavatra(*). Một phức hợp nhịp mềm tạo ra nhịp lượn sóng.
c. Borim Publishing house and Marionette Theater, Paju, Korea, 2003. Architecture Studio Himma. Lặp lại các tuyến đứng theo cách biến đổi dần đã tạo ra đường lượn sóng, bề mặt cong ghềnh cho công trình.
Trong việc tạo nhịp điệu giao thoa thì hình dạng của đơn vị cơ sở để tạo sự lặp lại rất quan trọng. Hình dạng này cần đáp ứng được khả năng lồng ghép đa dạng, với nhiều giải pháp về hướng nhằm tạo tính nhiều vẻ và cả sự bền chặt về cơ học cho tổng thể. Hình 4.29 là một số ví dụ tổ chức hình thể, hình dạng kiểu nhịp giao thoa của tự nhiên và vật dụng. Với nghệ thuật kiến trúc, tổ chức nhịp giao thoa được thể hiện cả trong cách tổ chức mặt bằng và hình khối.
Thủ pháp tạo nhịp điệu là cách thức hữu hiệu và hay được dùng trong nghệ thuật tạo hình. Tuy nhiên cần lưu ý việc tạo nhịp nhằm: hướng tới tính trật tự, sự thống nhất, tính quy luật của việc phối ghép hình dạng, hình thể nhưng cũng dễ dẫn đến hệ quả là sự buồn tẻ, đơn điệu khi quá lạm dụng. Vì vậy để có được tính đa dạng và thú vị về thị giác cần chú ý: cắt đoạn nhịp điệu, nhấn mạnh một vài bộ phận, chi tiết trong nhịp điệu, hay tạo yếu tố dị biệt trong tổ hợp. Phương cách này nhằm tạo nghỉ ngơi, yên tĩnh hoặc phá bỏ sự đồng điệu do lặp lại quá dài một vài yếu tố tạo hình nào đó.


Hình 4.29: Nhịp điệu giao thoa
a. Các nhánh thân cây cài lồng vào nhau tạo ra nhịp giao thoa đẳng hướng.
b. Một dạng cấu trúc đan sợi, nhịp giao thoa tạo nhiều hệ, phát triển đa hướng.
c. Nhịp giao thoa xuất hiện trên cơ sở một hệ tuyến cong cài lồng tương đối tự do (nguồn internet).
d. Một hợp nét thẳng và cong tạo nên nhịp giao thoa (nguồn internet).
e. Hai hệ tuyến zic-zắc tạo nên nhịp giao thoa (nguồn internet).
Hình 4.29f: Sắp xếp đá kiểu nhịp điệu giao thoa.
Hình 4.29g: Một góc tấm đan len. Một phức hợp tuyến tổ chức theo cách cài lồng so le tạo ra nhịp giao thoa.
Hình 4.29h: Weich Bauer/Ortis. Residential DNA. Austria.2001.
Các khối dạng chồng xếp theo kiểu cài lồng. Sự lặp lại và vươn xa của các khối tăng thêm hiệu quả động cho nhịp giao thoa.
* Bài tập thực hành 4.4: Nhịp giao thoa
Tạo nhịp giao thoa thông qua sử dụng tuyến, diện. Tổ hợp có thể được phát triển theo nhóm kiểu tán xạ, tuyến tính, kiểu mạng... Xem ví dụ hình 4.30.

Hình 4.30: Nhịp giao thoa
a. Nhịp giao thoa theo phương ngang và đứng.
b. Nhịp giao thoa phát triển theo một hướng.
c-d. Nhịp phát triển theo phương ngang.
e-f. Nhịp phát triển đa hướng.
g. Nhịp phát triển đa hướng.
h. Nhịp phát triển tán xạ.

Hình 4.31: Henri Matisse. The Dance. Sơn dầu (260 x 391cm), 1910
Họa sĩ đã đơn giản hóa tất cả các yếu tố: hình thể các nhân vật, màu sắc, các chi tiết mặc dù cũng được vẽ trên khổ tranh lớn. Toàn bộ đều hướng tới sự nhịp nhàng, uyển chuyển, trạng thái động của tác phẩm.

Hình 4.32: Robert Morris. Ohne Titel, 1967. Chất liệu tổng hợp (244 x 244 x 61cm)
Tác phẩm hình thành từ hai mô-đun giống hệt nhau dạng khối lăng trụ. Một mô-đun đứng vững chắc, một mô-đun mang dáng vẻ chông chênh.


Hình 4.33: Luminous House. Kagawa, Japan, 2011. Shinichi Ogawa & Associates. Một căn nhà ở một tầng với hình thức bên ngoài và nội thất theo phong cách tối thiểu.
a. Ảnh bên ngoài lúc trời tối.
b. Nội thất với thiết bị đơn giản, gam màu trắng sữa làm chủ đạo.
c. Góc nhìn phòng khách và sân trong.

Hình 4.34: Tanatorio Municipal de Terassa. Barcelona, Spain, 2002. BAAS Architects
a. Hình phối cảnh bên ngoài. Vẻ thanh thoát nhờ sự đơn giản về hình khối, đường nét, chất liệu, màu sắc cùng tỉ lệ hài hòa giữa các diện.
b. Nội thất khu phòng đợi đơn giản tối thiểu, không trang trí.

Hình 4.35: Nelsonatkins Museum of art in Kasas City, USA, 2006. Steven Holl(*)
a. Hình phối cảnh ban ngày. Khối hình đơn giản màu trắng, cảnh quan tĩnh lặng với các diện... và hồ lớn.
b. Hình phối cảnh ban đêm. Khối hình trắng kiểu dạng thủy tinh làm tôn vẻ thanh khiết cho công trình.

Hình 4.35c: Hệ vòm cong lấy ánh sáng tự nhiên hướng tới vẻ đẹp từ cấu trúc không trang trí.
Hình 4.35d: Không gian kiểu tầng bậc, các tuyến diện, khối đan xen. Vẻ đơn sắc và ít loại vật liệu không làm giảm tính biểu hiện của tác phẩm.
6. Tiết chế:
Trong quá trình tạo hình, các họa sĩ, kiến trúc sư, nhà thiết kế tạo dáng đưa các yếu tố thị giác, các hình ảnh khác nhau vào tác phẩm và đôi khi có thể dẫn tới sự phức tạp không cần thiết. Sự phức tạp này nhìn chung xuất phát từ hai nguyên nhân:
- Muốn tác phẩm nói lên được nhiều vấn đề hoặc mang nhiều ngữ nghĩa khác nhau.
- Dùng quá nhiều các hình thức, hay kiểu dạng cấu trúc để thể hiện tính đa nghĩa, tính đa năng của tác phẩm cũng như để liên kết các phần, các bộ phận vốn rất đa dạng và rời rạc của tổ hợp.
Biểu hiện cụ thể là những hình, hình thể cần diện rộng, cần tính đơn giản lại bị chia cắt, xuất hiện nhiều chi tiết rườm rà, nhiều ngữ nghĩa lẫn kiểu dáng. Ngay cả sự cấu kết giữa các phần cũng trở nên thừa và khó hiểu. Việc phức tạp này có thể sẽ dẫn tới tính thiếu đồng nhất của toàn cục, hay chệch hưởng với suy nghĩ, ý đồ ban đầu.
Để giảm bớt tính phức tạp, cần điều tiết, tiết chế các dạng hình thức khác nhau và trở lại với tính cốt lõi về hình thức cũng như nội dung, nên loại bỏ bớt những chi tiết rườm rà, các yếu tố dị biệt.
Tuy vậy, sự điều tiết - tiết chế các chi tiết, hình dạng, hình thể, hay hình ảnh không phải dễ tuân theo và thực hiện. Lí do các họa sĩ, kiến trúc sư, nhà tạo dáng trong quá trình sáng tạo của mình thường xuất hiện tức thời nhiều vấn đề cần giải quyết, cần quan tâm và đôi khi mải miết xử lí cục bộ mà quên đi tính toàn cục. Do đó việc tiết chế, các chi tiết nào đó nhằm hướng tới sự tập trung, tính rõ ràng tạo sự thống nhất là vấn đề cần đặt ra và hướng tới.
Sự tiết chế không có quy chuẩn, nó phụ thuộc nhiều vào trực giác của nghệ sĩ, nhưng về mặt lí thuyết khi thực hiện cần lưu ý:
+ Giảm bớt các chi tiết dị hình.
+ Tránh có quá nhiều chi tiết đối nghịch nhau về chiều hướng, mẫu hình, mô tip... mà lại tương đương nhau về kích cỡ.
+ Tránh dàn trải đều các chi tiết vì điểm này dẫn tới sự mất tập trung thị giác, khó phân chia trọng tâm, có thể dẫn tới sự hỗn loạn trong bố cục.
+ Những yếu tố ví dụ như nét, diện chia cắt tác phẩm nên tiết giảm.
+ Cần có giải pháp điều hòa, hòa hợp, chuyển tiếp các phần riêng lẻ và khác biệt.
Khi sáng tác tuân theo lối tiết chế cần lưu ý sự tiết chế có thể là áp lực và có thể dẫn tới sự đơn điệu của tác phẩm. Việc tinh giản, gọt đẽo, loại trừ bớt các hình dạng, hình ảnh dễ dẫn tới tính trừu tượng, gây sự khó hiểu về cả hình lẫn ngữ nghĩa. Chất lượng tinh giản, tiết chế phụ thuộc nhiều vào kinh nghiệm của họa sĩ, kiến trúc sư, nhà thiết kế.
Về mặt thẩm mĩ, về mặt hữu dụng chỉ được công nhận là hiệu quả khi sự tinh giảm của người vẽ, người thiết kế dung hòa với khả năng nhận thức của người xem, người sử dụng. Hình ảnh, sản phẩm đã tiết chế phải như thế nào đó để người thưởng thức cảm thụ, tri giác được dễ dàng và thấy cả sự thú vị trong phép tiết chế này.
Trong lịch sử nghệ thuật nhất là nghệ thuật hiện đại, tính tiết chế được nhiều họa sĩ, kiến trúc sư áp dụng. Henri Matisse một trong những người họa sĩ có ảnh hưởng lớn nhất tới nghệ thuật thế kỉ XX ngay từ thời kì đầu cách tân đã hướng tới lối vẽ đơn giản tiết kiệm (xem ví dụ hình 4.31). Hay như những nghệ sĩ điêu khắc theo phong cách tối thiểu (minimalist style) và cách sử dụng hình học đơn giản nghiêm khắc, không trang trí, không nhiều chi tiết để tạo ra tác phẩm ba chiều đa nghĩa hay trừu tượng (xem ví dụ hình 4.32). Hoặc những tác phẩm kiến trúc, đặc biệt kiến trúc nhà ở theo xu hướng tối giản (minimalism). Với cách tổ chức không gian khúc chiết, cô đọng về hình khối chất liệu và thiết bị vật dụng nhưng lại gây ấn tượng mạnh về tạo hình, về cách gây tổ chức không gian sống. (Xem ví dụ 4.33; 4.34; 4.35).
Le Corbusier quan niệm công trình kiến trúc xây nên là để con người sử dụng hằng ngày. Vì vậy để đạt được tính ứng dụng, sự hợp lí cần đưa kích thước con người vào phép đo tạo dựng công trình.
Le Corbusier lập ra hệ thống thước tỉ lệ giữa các phần cơ thể con người theo quy luật thiết diện vàng và chuỗi số cộng. Lấy hệ thước này làm cơ sở cho phép dựng hình không gian kiến trúc cũng như thiết kế các đồ vật dụng.
Le Corbusier gọi thước của mình là modulor (thước vàng). Lấy toán học với con số vàng làm cơ sở và xây dựng liên hệ thang mang tính tầng bậc trên nguyên tắc tỉ lệ của con người. Ban đầu ông lấy tầm vóc con người là 175cm để xây dựng lên hai thang thiết diện vàng. Sau đó ông cố gắng dung hòa hệ đo bằng mét (m) với số đo bằng foot và lấy chiều cao người đàn ông cao 183cm (tức ở foot - 182,88cm) làm cơ sở.
Với tư thế đứng giơ tay rồi xác định sự liên quan giữa chân, bụng, đầu, các ngón tay của bàn tay giơ cao. Tạo nên 3 độ dài theo dãy số cộng có tỉ lệ vàng là: 1130; 698; 432cm.
Từ rốn trở xuống là dãy số cộng giảm dần. Chuỗi số bắt đầu từ 1130 và gồm các số sau đây: 698; 432; 266; 165; 102; 63; 39; 24; 15; 9; 6mm ( ở số hạng 266 có sai số 1mm).
Le Corbusier đặt tên cho thang gắn liền với kích thước người đàn ông cao 183cm là “thang đỏ” . Thang bổ túc thứ hai có tên là “thang xanh”, được bắt đầu từ số 2260 và có giá trị tương ứng gấp đôi thang đỏ. Có dạng như sau: 11; 18; 30; 48; 78; 126; 204; 330; 863; 1397; 2260mm...
Những kích thước hình thành trên cơ sở thang xanh và thang đỏ được quy trong đến cen-ti-mét, tuân theo quy luật thiết diện vàng, chuỗi số cộng đồng thời đơn giản hóa gần gũi với kích thước con người. Dãy đỏ bắt đầu với đơn vị chuẩn là 1.13cm bằng 1M, dãy xanh với đơn vị chuẩn là 2.26cm tức 2M:
Thang đỏ:\6\10\16\27\43\70\113\183\296\479...
Thang xanh:\13\20\33\53\86\140\226\366\592\957...
Hai thang trong đó mô-đun của Le Corbusier đã tạo ra dãy số nhằm mang lại tính hữu dụng, sự phối kết hài hòa giữa các phần với nhau trong thiết kế từ không gian đô thị, không gian hạng mục của kiến trúc cho tới các vật dụng hằng ngày.
Modulor được nhiều nhà hoạt động nghệ thuật và văn hóa đánh giá cao và coi đó là sự đóng góp quan trọng trong hệ thống lí thuyết tỉ lệ.
Hình 4.45 là hình vẽ modulor và minh họa ứng dụng cụ thể của modulor tương ứng với các tư thế chính của hoạt động con người (cao 183cm).
7. Tỷ lệ:
Một phần lịch sử toán học và nghệ thuật từ thời Cổ đại là quá trình quan sát - phân tích và lí thuyết hóa những nguyên tắc về tỉ lệ, tỉ lệ cân xứng, chuỗi số (Ratio, Proportion, Progression) của những sự vật trong môi trường xung quanh.
Mục đích của tất cả các lí thuyết về tỉ lệ này nhằm hiểu và tạo nên cảm giác về sự trật tự, tính cân bằng, vẻ hài hòa giữa các thành phần khác nhau trong một bố cục hay một khung trường nhìn cụ thể.
Một hệ thống tỉ lệ cân xứng hay chuỗi số thiết lập những quan hệ nhất quán giữa các phần của một bộ phận, giữa các bộ phận với nhau cũng như giữa các bộ phận và tổng thể. Trong phần lớn trường hợp, các quan hệ tỉ lệ này người xem không nhận thức được ngay lập tức, nhưng tính trật tự thị giác có thể thấy qua việc lặp lại một hình dạng, một số yếu tố hay một kiểu cấu trúc nào đó.
Có thể phân ra ba cách thức nghiên cứu, ứng dụng hệ thống tỉ lệ để tạo ra tính cân xứng cho một vật thể hoặc hợp nhóm các vật thể là: hình học, đại số và điều hòa. Hệ hình học dựa trên các phép dựng, phép chia hình học, lấy các hình cơ bản (vuông, chữ nhật , tam giác, tròn...) làm cơ sở. Hệ đại số dựa vào hướng tiếp cận các hình theo kinh nghiệm, theo mẫu hình. Hệ điều hòa được xây dựng từ quy luật toán học trừu tượng (ví dụ các chuỗi số ).
Hình 4.36 là các minh họa về việc sử dụng các quan hệ tỉ lệ trong dựng hình, nghiên cứu tự nhiên và tạo dáng.
Cần hiểu hệ thống tỉ lệ (Ratio), tỉ lệ cân xứng (Proportion), chuỗi số (Progression) là phạm trù, là các khái niệm tương đối phức tạp với những nguyên tắc có thể là bí ẩn hoặc có tính chất không rõ ràng.
Các lí thuyết về tỉ lệ được phát triển trong nhiều nghìn năm lịch sử. Với mong muốn tạo ra cái “hoàn hảo” cho sự vật. Tuy nhiên ở thời kì nào đó cũng phụ thuộc vào một loạt các yếu tố mang tính xã hội và kĩ thuật.
Ví dụ:
+ Bối cảnh xã hội, giai đoạn lịch sử, ý thức tư tưởng tôn giáo, đặc tính văn hóa vùng miền.
+ Phụ thuộc vào kĩ thuật, vật liệu, kết cấu xây dựng đối với lĩnh vực kiến trúc và điêu khắc.
+ Kích thước vật lí về tỉ lệ, tỉ lệ cân xứng sẽ không hoàn toàn chính xác, nó bị biến dạng bởi góc nhìn phối cảnh trong không gian ba chiều, hay khi cảm thụ hình thể ở trạng thái động.
Những nguyên tắc về tỉ lệ cân xứng, chuỗi số cùng giá trị thực tế của nó luôn được ứng dụng trong mĩ thuật, kiến trúc và thiết kế tạo dáng qua nhiều thời đại. Nhưng lưu ý rằng đây không phải là công thức có thể áp dụng dễ dàng cho mọi trường hợp. Trong quá trình tạo hình cần kết hợp những nghiên cứu cụ thể, cho từng khung cảnh từng loại hình tổ hợp riêng. Ví như trong thiết kế một công trình kiến trúc phức tạp thì việc kết nối hệ thống tỉ lệ với tổ chức hệ cấu trúc đa chiều là không hề đơn giản.
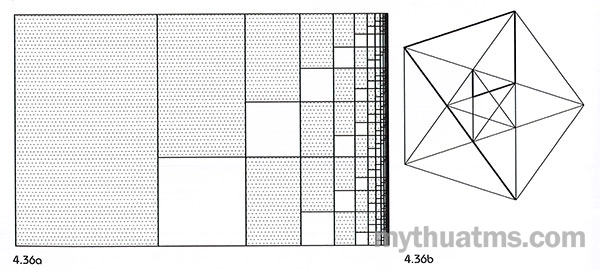
Hình 4.36: Nghiên cứu và ứng dụng tỉ lệ cân xứng
a. Chia nội tại hình chữ nhật vàng tạo ra nhịp tiệm tiến.
Hình 4.36b: Hình ngũ giác đều với ngôi sao năm cánh tạo nét đậm gấp khúc nhịp nhàng uyển chuyển.
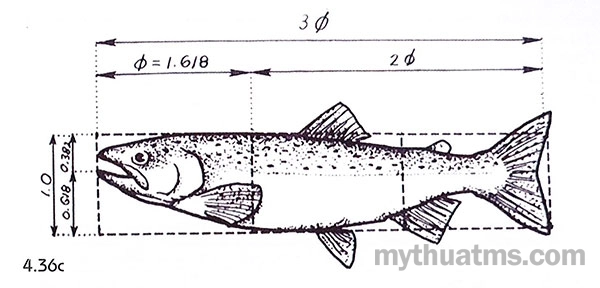
Hình 4.36c: Đo đạc con cá hồi liên quan đến con số vàng.
* Tỉ lệ vàng - Hình chữ nhật vàng: Triết học Hy Lạp cổ đại bày tỏ và có niềm tin rằng toán học là lực điều khiển vũ trụ. Họ tin tưởng mối quan hệ giữa các con số phản ánh vẻ hài hòa về cấu trúc của vạn vật.
Hệ thống toán học về tỉ lệ cân xứng (Proportion) được khởi nguồn với quan niệm “tất cả là các con số”. Con số cho thấy trật tự của tổng thể.
Vì vậy, từ buổi đầu họ đã thiết lập một quy tắc vàng hay còn gọi là tỉ lệ vàng (Golden section) để trình bày, diễn giải những lí tưởng về sự cân bằng, cân xứng trong đời sống vạn vật và nghệ thuật.
Tỉ lệ vàng chỉ ra nguyên tắc liên kết của bộ phận nhỏ với bộ phận lớn hơn và phần lớn liên quan đến toàn bộ.
Quan điểm trên được khởi nguồn thông qua cách chia một đoạn thẳng hay còn gọi là điểm giữa hai thái cực. Cụ thể, khi đoạn thẳng AB được chia làm hai phần bởi điểm C, thì tỉ số giữa AC và AB bẳng tỉ số giữa CB và AC. Điều đó là AC: AB = CB: AC và có giá trị 1: 1,618 (xem hình 4.37). Tỉ lệ này gọi là tỉ lệ vàng hay còn gọi là tỉ lệ thần thánh. Và định số 6180 là con số để hình thành nên một hình thể hay một tổ hợp hài hòa.
Đưa khái niệm và định số 6180 vào hình học phẳng, người Hy Lạp tìm ra một hình chữ nhật có tỉ lệ đẹp nhất từ hình vuông và gọi là hình chữ nhật vàng (Golden rectangle). Cách dựng hình này xem hình vẽ 4.37c. Một đặc điểm làm cho hình chữ nhật tỉ lệ vàng khác lạ là khi một hình vuông được thiết kế trên cạnh ngắn của hình chữ nhật gốc, phần còn lại cũng là hình chữ nhật có tỉ lệ vàng, nhưng nhỏ hơn.
Do đặc điểm đặc biệt mà hình chữ nhật vàng còn được gọi là hình chữ nhật “xoắn ốc vuông”, bằng cách chia một hình chữ nhật vàng theo cách chỉ giữ lại phần hình vuông của hình chữ nhật vàng, sẽ có hình vuông sắp xếp theo kiểu xoắn ốc. Tiếp đó có thể sử dụng các cung tròn với bán kính lần lượt bằng các cạnh hình vuông tương ứng sẽ lập nên một hình vòng xoáy ốc.
Tỉ lệ vàng, hình chữ nhật vàng có những đặc tính đại số và hình học đáng lưu ý và thú vị. Nó hiện hữu trong rất nhiều cấu trúc hình thái tổ chức tự nhiên cũng như kiến trúc và mĩ thuật. Hình 4.38 là các ví dụ.
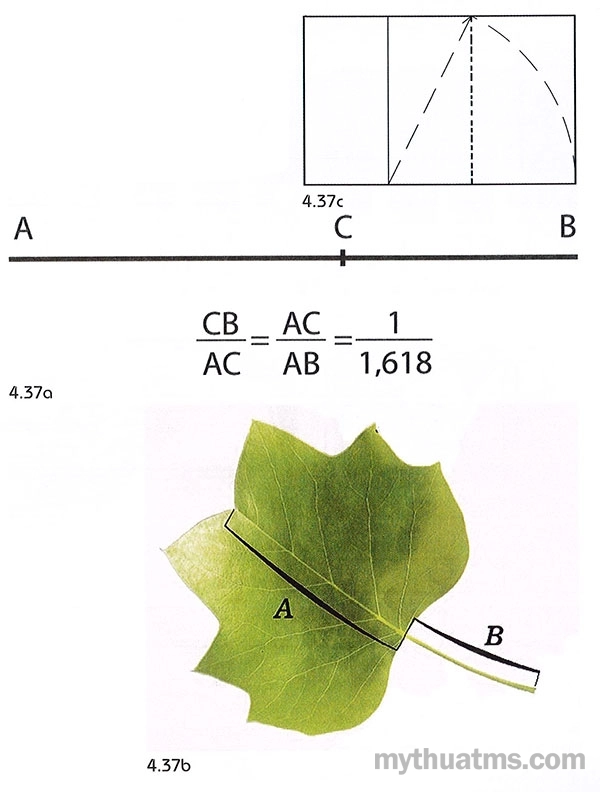
Hình 4.37: Điểm chia giữa hai thái cực
a. Điểm chia đoạn thẳng AB theo tỉ lệ vàng.
b. Cuống lá và độ dài lá quan hệ theo tỉ lệ vàng.
* Bài thực hành 4.5: Tỉ lệ và thế giới tự nhiên
Sưu tầm, đo đạc, vẽ sơ đồ các vật dụng, các hình thể giới tự nhiên có tổ chức theo tỉ lệ vàng (xem ví dụ hình 4.38).

Hình 4.38: Hình dạng có tỉ lệ vàng
a. Đền Parthenon. Mặt chính của đền nằm gọn trong hình chữ nhật vàng. Phân vị ngang nằm trong các hình chia nhỏ nội tại theo quy luật vàng.
b. Bức tranh “La Gioconda” của danh họa Leonardo da Vinci được sắp xếp theo hình chữ nhật tỉ lệ vàng.
c. Hygeria, nữ thần sức khỏe. Tượng Hy Lạp cổ. Nét đẹp chuẩn mực của khuôn mặt có nhiều phần tương quan theo tỉ lệ vàng.
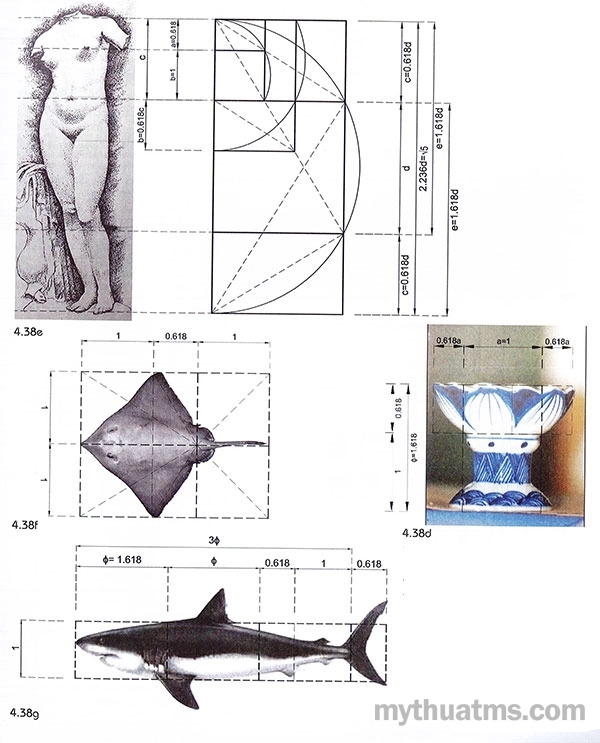
Hình 4.38d: Đồ đựng gốm Bát Tràng - Việt Nam. Độ rộng miệng bát, chân đế và thành bát tương quan tỉ lệ vàng.
Hình 4.38e: Tượng nữ thần sắc đẹp ở Cyrene (Aphorodite of Cyrene). Mẫu hình người Hi Lạp cổ về vẻ đẹp hình thể, người phụ nữ.
Hình 4.38f: Con cá đuối biển. Hình dạng bản dẹt. Các phần có tương quan, phân đoạn theo tỉ lệ vàng đơn giản.
Hình 4.38g: Cá mập biển. Thân dạng trụ - tương quan tỉ lệ vàng.
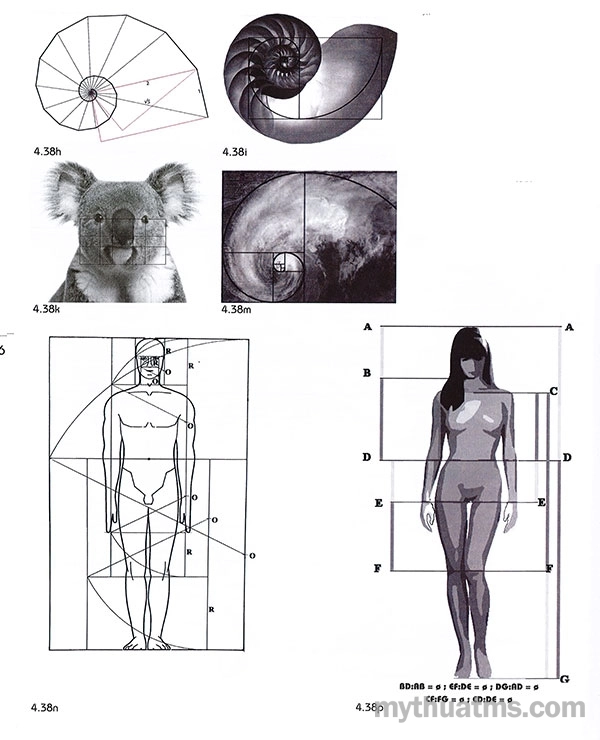
4.38h: Đường xoắn ốc có nguồn từ hình chữ nhật số căn 5.
4.38i: Đường xoắn ốc vàng (chữ nhật vàng) đồng điệu với đường xoắn cấu trúc vách vỏ của ốc anh vũ.
4.38k: Gấu Koala. Khuôn mặt với chi tiết được tổ chức theo hình chữ nhật vàng.
4.38m: Ảnh chụp vệ tinh. Đám mây hình thành từ cơn bão có dạng hình xoáy ốc vàng.
4.38n: Tỉ lệ vàng, hình chữ nhật vàng và cơ thể người đàn ông (nguồn: Basic Visual Concepts and Principles).
4.38p: Tỉ lệ vàng cơ thể người phụ nữ
* Bài thực hành dạng 4.6: Tạo hình dạng có tỉ lệ vàng
1. Hợp nhóm chia cắt hình cơ bản theo tỉ lệ vàng (xem các ví dụ hình 4.39).
2. Tạo một hình dạng, hình thể, một vật dụng có tương quan tỉ lệ vàng (ví dụ hình 4.38d).
Bài tập có thể làm dưới dạng đồ họa hay mô hình.
- Chuỗi fibonacci: Lí tưởng của người Hi Lạp cổ về những con số vàng kéo dài qua dòng lịch sử và được các thế hệ tiếp theo bổ sung. Leonardo Fibonacci nhà toán học Ý thời Trung cổ đã định ra một chuỗi những con số theo quy luật. Chuỗi số này gọi là chuỗi số cộng hay được gọi là chuỗi Fibonacci. Đây là chuỗi số được thực hiện bằng những tương quan số nguyên trên cơ sở của tỉ lệ vàng, tiết diện vàng.
Dãy số Fibonacci là dãy vô hạn các số tự nhiên bắt đầu bằng hai số 1 và 1, các số sau được thiết lập theo quy tắc mỗi số luôn vằng tổng hai số trước nó. Dãy số đó là:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144...
Chuỗi Fibonacci là chuỗi số cộng đơn giản, được nhiều người biết đến và ứng dụng rất rộng rãi. Chuỗi này liên hệ với tỉ lệ vàng. Tỉ lệ của hai số liền sau kề sau số 3 trong chuỗi số luôn có hướng tiến đến tỉ lệ vàng khi dãy số tiến đến vô cực (1,6180...).
Với tỉ lệ 1: 16180 người ta có thể bắt đầu tạo ra một chuỗi mới từ bất kì con số nào theo quy tắc cộng. Ví dụ, bắt đầu từ con số 10, nhân nó với 1,6180 để con số 16 (đã đơn giản hóa) từ số này theo quy luật cộng hai con số sẽ có chuỗi số: 10, 16, 26, 42, 68,... chuỗi này có tỉ số hai số liền kề là tỉ lệ vàng và có thể ứng dụng trong điều kiện riêng nào đó.
Chuỗi Fibonacci phản ánh quá trình phát triển và cấu trúc của thế giới tự nhiên. Chuỗi này xuất hiện ở khắp nơi. Tính chất sinh động tăng giảm của chuỗi đã tạo ra khả năng ứng dụng rất đa dạng mang nhiều vẻ lí thú. Có thể dẫn ra nhiều ví dụ về chuỗi này trong tự nhiên cũng như trong ghép tạo hình nghệ thuật.
Các số Fibonacci xuất hiện nhiều trong những bông hoa, hầu hết số cách hoa trong một bông hay một lớp cánh là các số 1, 3, 5, 8, 13, 21... Loài cúc có thể có 34, 55 hay thậm chí 89 cánh hoa (xem hình 4.40).

Hình 4.39: Hợp nhóm các hình có tỉ lệ vàng

Hình 4.40: Chuỗi Fibonacci và số lượn cánh hoa (a - e)
Số lượng cánh hoa trên một bông hoa là 1, 3, 5, 7, 13.
Con số của dãy Fibonacci cũng xuất hiện trên nụ của bông hoa hướng dương. Nụ này được kết thành hai hệ tuyến cong hướng tâm. Một hệ uốn ngược chiều kim đồng hồ còn hệ kia thuận chiều kim đồng hồ. Số các đường gắn ngược chiều với kim đồng hồ thường là 34 còn chiều kim đồng hồ là 55, có khi là 55 và 89 hay 89 và 144. Tất cả các con số này đều nằm trên chuỗi số Fibonacci và kế tiếp nhau. Tỉ số của chúng tiệm cận con số vàng 1,618. Hình 4.41a là sơ đồ và ảnh chụp nụ bông hoa hướng dương có các số đường xoắn ngược và xuôi chiều kim đồng hồ là 21 và 34 . Hình 4.41b là nụ hoa có các đường xoắn là 34 và 55.

Hình 4.41: Nụ hoa hướng dương và chuỗi Fibonacci (nguồn internet)
a. Số đường xoắn ngược và xuôi chiều kim đồng hồ là 21 và 34.
b. Số đường xoắn ngược và xuôi chiều kim đồng hồ là 34 và 55.
* Xoắn ốc Fibonacci: Các số Fibonacci thực sự có mặt trong tự nhiên. Ví dụ các tuyến cấu trúc của hạt hoa hướng dương, hình dạng những cơn bão, hay dải ngân hà (xem hình 4.41 và 4.42).
Chúng được sắp xếp theo quy luật xoắn ốc, các phần tương quan theo con số cộng Fibonacci.
Xoắn ốc này được tập hợp từ một phần cung tròn, được vẽ bên trong một ma trận gồm những hình vuông có các cạnh là các con số Fibonacci. Các hình vuông khớp với nhau do bản chất của dãy số cộng. Trong đó dãy số tiếp theo bằng tổng của hai số đứng trước nó. Xem hình 4.43.

Hình 4.42: Xoắn ốc Fibonacci của dải ngân hà Messier 74 (nguồn internet)
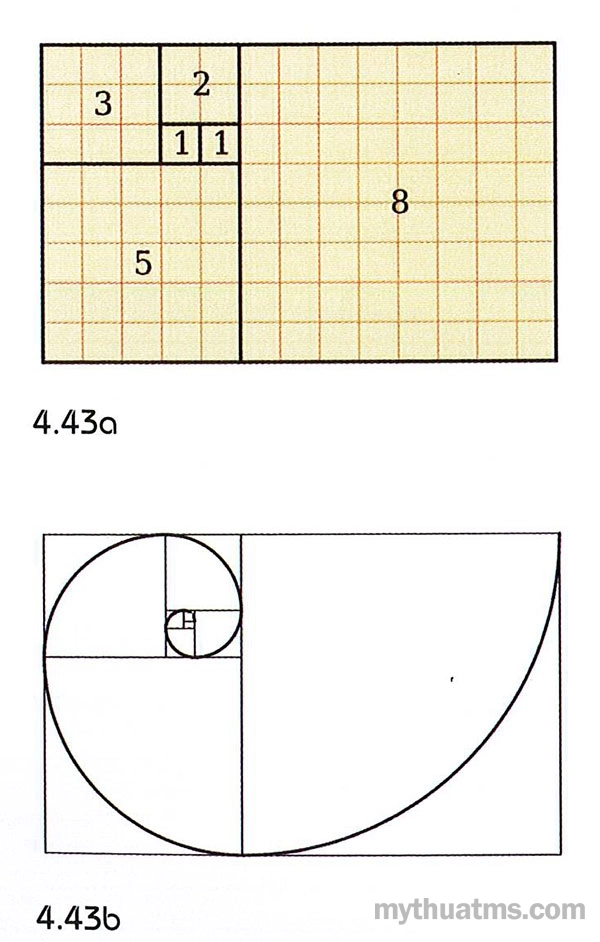
Hình 4.43: Xoắn ốc Fibonacci và hình chữ nhật vàng
a. Các cạnh hình vuông có độ dài tương ứng với chuỗi Fibonacci.
b. Tiếp nối các cung tròn tạo ra xoắn ốc Fibonacci.
>>> Nguyên tắc tổ hợp (Phần 1)
>>> Nguyên tắc tâm lý hình học trong TK logo
>>> Nguyên tắc "Chiaroscuro" trong vẽ tranh