Cấu trúc các hình thể
Thường khi tạo hình một hình thể đơn vị (unit form), người ta ít chút trọng tới cấu trúc nội tại của bản thân hình đơn. Nhưng khi hợp nhóm, chúng có trật tự cần theo một sơ đồ cấu trúc nào đó.
Cấu trúc (structure) là khái niệm để chỉ cách sắp xếp, tổ chức, khống chế các hình thể (form) hình dạng (shape) theo một quy luật nào đó. Cấu trúc trong tạo hình thường được hiểu dưới dạng tuyến, dạng mạng hai hay ba chiều.
Hình 5.1.1a là cấu trúc sắp xếp vẩy một con cá rồng. hình 5.1.1b, các hình tròn, hình elip được bố trí trong khuôn khổ hệ tuyến cấu trúc (structure lines) dạng lưới tam giác tự do.


Hình 5.1.1:
a. Cấu trúc vẩy con cá rồng là hệ lưới có bờ cạnh cong.
b. Hợp nhóm các hình tròn, hình elip (các hình này là các hình đơn vị). Hệ cấu trúc mạng là hệ lưới tam giác.
a. Tuyến và lưới cấu trúc: Trong thiết kế tạo hình và cả hình ảnh thực của thế giới tự nhiên, phần lớn tuyến cấu trúc (structure lines) là ảo, là vô hình (invisible structure) kể cả cấu trúc kiểu cân xứng, đều đặn. Các tuyến thường do người thiết kế, người vẽ, người xem tưởng tượng và sơ đồ hóa ra để dễ sắp đặt các hình đơn vị. Hình 5.1.2 vẽ các hình tròn được xếp đều đặn theo hệ lưới trong một hình chữ nhật (hình 5.1.2a), hệ lưới sẽ được người xem tưởng tượng ra (hình 5.1.2b).
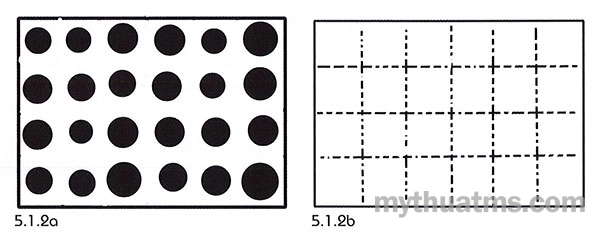
Hình 5.1.2: Lưới cấu trúc
a. Các hình tròn đen được bố trí đều đặn trong một hình chữ nhật.
b. Hệ mạng lưới được tưởng tượng ra (lưới ảo).
Thế giới tự nhiên phần lớn có tuyến cấu trúc ẩn đi hoặc mờ nhạt không rõ ràng, nhưng nhà thiết kế đôi khi lại thích dùng lưới cấu trúc hữu hình (visible structrue), tức nó hiện rõ lên. Khi đó tuyến cấu trcus có độ dày mảnh khác nhau, khi âm bản khi dương bản, khi là nét liền mạch khi nét đứt quãng (hình 5.1.3).
b. Mạng lưới cơ sở và biến thể: Trên cơ sở mạng lưới ô vuông cơ sở, bằng phương pháp lặp lại, biến hình, co giãn… có các dạng biến thể cơ bản sau:
a. Mạng lưới cơ sở hình vuông (hình 5.1.4a).
b. Mạng lưới ô chữ nhật (hình 5.1.4b).
c. Mạng tứ giác xiên chéo (hình 5.1.4c).

Hình 5.1.3: Kiểu nét của lưới cấu trúc
a. Lưới hữu hình, nét liền dương bản.
b. Lưới hữu hình âm bản.
c. Lưới đứt quãng
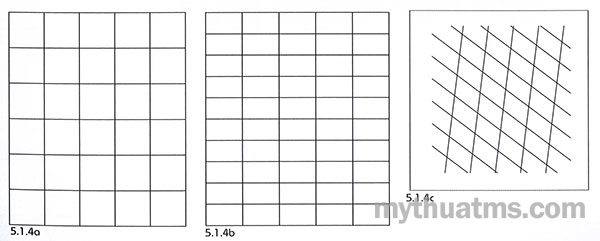
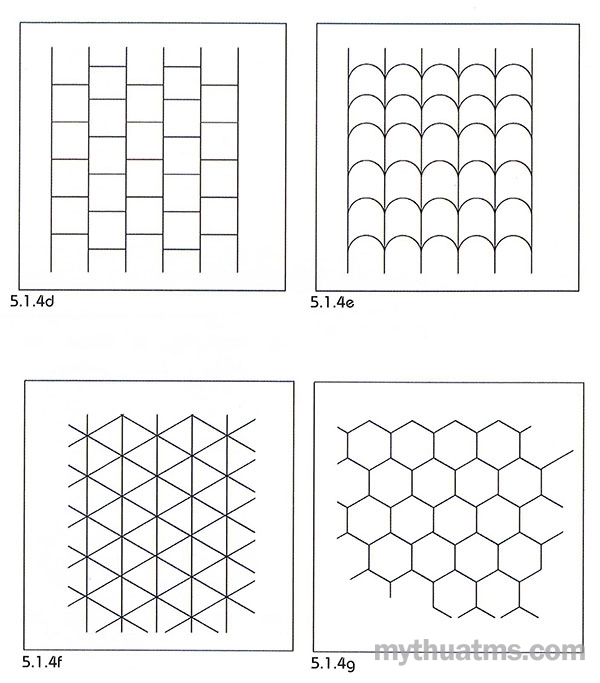
d. Mạng so le, trượt hình (hình 5.1.4d).
e. Mạng lưới có bờ cạnh cong (hình 5.1.4e).
f. Mạng lưới tam giác (hình 5.1.4f).
g. Mạng lục giác (hình 5.1.4g).
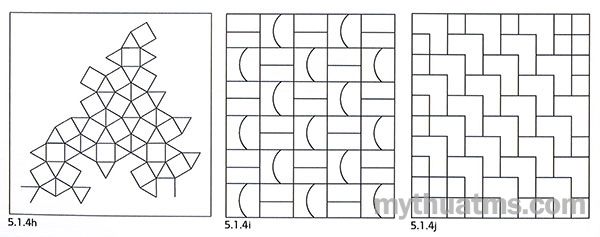
h. Mạng đa lặp hình tam giác và hình vuông (hình 5.1.4h).
i. Mạng chia nội tại (hình 5.1.4i).
j. Mạng cài lồng giao thoa (hình 5.1.4k).
c. Mạng không gian ba chiều: Mạng không gian ba chiều thường được hình thành trên cơ sở ô gốc là khối lập phương. Biến thể của nó thể hiện cụ thể ở dạng thức: ô không gian cơ sở, hợp nhóm các khối đa diện đều và bán đều hay phép dùng diện đơn tạo không gian.
Hình 5.1.5 là các ảnh chụp mô hình tạo dựng cấu trúc ba chiều dạng ô lưới.

Hình 5.1.5: Mạng ba chiều
a. Mạng 3 chiều hình thành trên ô gốc là hình lập phương, mỗi ô gốc được chia nội tại bên trong (Bài tập sinh viên).
b. Mạng không gian được hình thành từ mạng gốc có 4 mặt tam giác được ghép nối đều đặn qua đỉnh và cạnh (Bài tập sinh viên).
c. Mạng được cấu tạo từ khối đa diện bán đều (mặt tam giác và lục giác) được đấu nối qua tiếp xúc các diện tam giác (Bài tập sinh viên).
d. Cấu trúc không mạng lưới: Cấu trúc không mạng lưới là cấu trúc mà các hình thể đơn vị bố cục sắp xếp không tuân theo hệ lưới cấu trúc hai hay ba chiều. Ví như kiểu tổ chức tập trung theo tuyến, theo điểm, kiểu tán xạ hay hình thức tổ chức tương phản hoặc kiểu phân rã…
Hình 5.1.6 là ví dụ về hợp nhóm các hình theo dạng không mạng lưới.

Hình 5.1.6: Cấu trúc không mạng, lưới…
a. Các hình dạng lá cây tập trung theo chiều dọc, cách bố trí tương đối tự do, không theo dạng lưới. Kiểu tập trung theo tuyến.
b. Các tuyến mảnh được bố cục tự do đa chiều hướng, độ mảnh dầy khác nhau, tổng thể như những hình người nhảy múa; kiểu tổ chức giao thoa cài lồng.
c. Các đơn vị khối tứ diện (mặt tam giác) có kích thước khác nhau tập trung gắn kết theo chuỗi gấp khúc, zíc-zắc (bài tập sinh viên).
d. Các đơn vị khối lập phương tập trung dầy đặc, chiều hướng khác nhau, vây xung quanh một vùng (bài tập sinh viên).
e. Các dạng hình cấu trúc: Các hình thể đơn vị (unit forms) khi kết hợp với nhau theo hay không theo mạng sẽ tạo ra các dáng vẻ hình thức khác nhau. Về mặt hình thức có các dạng sau:
- Cấu trúc cân xứng (formal structure) là dạng cấu trúc mà các hình đơn vị được tổ chức chặt chẽ theo hệ mạng nghiêm ngặt, chính xác. Hình thức thường đều đặn, có nhịp điệu, tỷ lệ rõ ràng.
Thủ pháp tạo ra cấu trúc cân xứng thể hiện dưới dạng thức: lặp lại (repetiton), biến đổi dần (gradation) và tán xạ (radiation).
Hình 5.1.7 là các minh họa kiểu cấu trúc cân xứng.

Hình 5.1.7: Cấu trúc cân xứng
a. Cấu trúc cân xứng – lặp lại các hình đơn vị, lặp y nguyên hình dạng theo các ô vuông đều đặn.
b. Cấu trúc cân xứng – biến đổi dần. Các hình đơn vị có kích thước thay đổi dần.
c. Cấu trúc cân xứng – kiểu tán xạ. Các hình đơn vị trong mỗi ô lưới thay đổi, lấy tâm làm gốc.
- Cấu trúc bán cân xứng (semi-formal structure): là dạng cấu trúc mà một phần các hình đơn vị không hoàn toàn giống nhau, chúng tương tự nhau hoặc được tổ chức không đều đặn. Nhưng các hình vẫn tuân theo một quy luật nào đó. Nó có thể được tổ chức theo dạng tuyến mạng đã biến thể hay không có tuyến mạng.
Dạng cấu trúc bán cân xứng thể hiện dưới dạng thức: kiểu tương tự (similarity) hay kiểu dị biệt (anomarly). Hình 5.1.8 là các minh họa kiểu cấu trúc bán cân xứng.
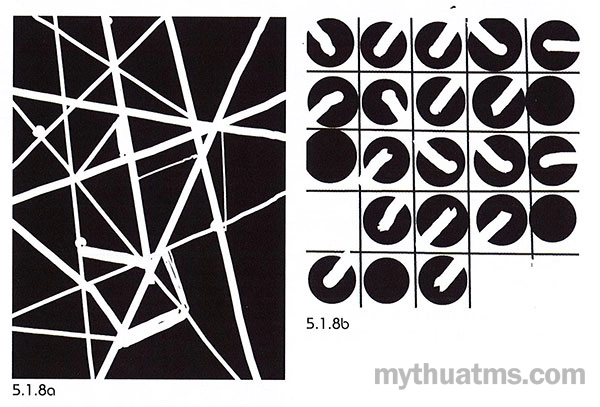

Hình 5.1.8: Cấu trúc bán cân xứng
a. Một dạng tương tự về cấu trúc (mạng tam giác).
b. Các hình tròn khuyết trong, quay chiều hướng khác nhau, chúng tương tự về hình dạng và được đặt trong hệ lưới ô vuông đều đặn, tạo ra cấu trúc bán cân xứng.
c. Tính bán cân xứng được tạo ra mặc dù có sự dị biệt nhỏ ở phần cuối các tuyến thẳng dọc, xuất hiện đường xoáy ốc tròn.
- Cấu trúc không cân xứng: là dạng cấu trúc mà các hình thể đơn vị không tuân theo hệ tuyến mạng, tuyến cấu trúc (structure lines). Cấu trúc dạng này thể hiện dưới dạng thức: tập trung – phân rã (concentration – de concentration), tương phản (contrast). Hình 5.1.9 là các minh họa kiểu cấu trúc không cân xứng.

Hình 5.1.9: Cấu trúc không cân xứng
a. Các hình vuông có đường bao dầy, mảnh khác nhau, chiều hướng khác nhau, bố cục tự do kiểu dàn trải tạo ra một bố cục động đa hướng.
b. Các tuyến có độ mảnh khác nhau, chồng chất lên nhau, chiều hướng luôn thay đổi và sắp xếp không tuân theo hệ mạng hay tuyến. Một bố cục phi cân bằng và rất động.
c. Một bố cục phi cân xứng do sự tương phản giữa đen và trắng, giữa mềm mại của hình với phẳng cứng của phông, giữa khoảng trống rộng và các khe nhỏ hẹp.
- Cấu trúc tĩnh (inactive structure): là dạng cấu trúc nhìn vào thấy ổn định, chắc chắn, tĩnh tại. Các hình đơn vị trong cấu trúc này được sắp xếp nghiêm ngặt trong hệ lưới tuyến, nó độc lập nằm trong ô lưới không can thiệp vào các ô khác liền kề và các hình đơn vị khác (xem hình 5.1.10).

- Cấu trúc động: Nếu xét dưới dạng tổ chức hợp nhóm kiểu mạng đều đặn, cấu trúc động (active structrue) là dạng cấu trúc mà các hình đơn vị được tổ chức dưới dạng hệ lưới tuyến, các tuyến có thể hiện rõ (visible structure) hay không hiện rõ (invisible structure), khi đó các hình đơn vị trong hệ tuyến này là nguyên nhân gây nên tính động của cấu trúc, nó có kích cỡ khác nhau, hình dạng khác nhau và vị trí trong ô lưới khác nhau. Có các nguyên nhân gây ra tính động dạng này như sau:
+ Động do màu sắc, sắc độ, chất liệu: Các hình đơn vị có thể giống nhau về hình dạng, vị trí trong hệ tuyến lưới nhưng lại khác nhau về màu sắc, sắc độ, chất liệu. Mỗi hình đơn vị tồn tại tương đối độc lập, và có thể xuất hiện sự hoán đổi phông – hình (hình 5.1.11).

Hình 5.1.11: Cấu trúc động do hình đơn vị khác nhau về màu, về chất liệu
a,b. Các hình tròn có kích cỡ và hình dạng giống nhau, đặt trong ô lưới đều đặn và tạo ra một cấu trúc động do sắc độ, màu sắc một số hình đơn vị khác nhau.
+ Động do kích cỡ, hình dạng, vị trí:
Trong mỗi ô, lưới cơ sở, hình đơn vị có thể được đặt ở vị trí khác nhau, có kích thước khác nhau, khi đó chúng có thể bị chia cắt, cài lồng vào nhau hay bị xô lệch, ô lưới có cảm giác bị phá vỡ một phần. Ví dụ: hình 5.1.12.

Hình 5.1.12: Cấu trúc động do thay đổi vị trí và hình dạng hình đơn vị
a. Một số hình vuông đen lệch khỏi vị trí trung tâm.
b. Một số hình tròn bị bờ cạnh ô lưới chia cắt, một số có hình dạng khác biệt.

Hình 5.1.13: Tổ chức các hình theo cách:
a. Lặp lại.
b. Biến đổi dần.
c. Tán xạ.
d. Tương tự.
e. Dị biệt.
f. Tập trung.
g. Phân rã.
h. Tương phản.
* Bài thực hành 5.1.1: Hệ lưới và biến thể
Tạo dựng một hệ lưới: tam giác, vuông, chữ nhật, ngũ giác, lục giác… hoặc hệ đa lặp. Trên cơ sở hệ lưới này tạo biến thể của nó theo cách thức sau:
- Khoét rỗng một phần hệ lưới để tạo các vùng trống có quy mô hình dạng khác nhau.
- Thay đổi hình dạng của ô cơ sở để tạo ra hợp nhóm ô lưới mới.
- Co kéo, ép nén hệ ô lưới.
- Dùng thủ pháp biến đổi dần ô cơ sở để làm thay đổi cấu trúc hệ lưới.
Sau khi tạo được hệ lưới, tô đen một phần các ô lưới để tập hợp thành dạng tuyến, dạng tập trung, tán xạ… của phần được tô đen. Xem các ví dụ hình 5.1.14 và 5.1.15.
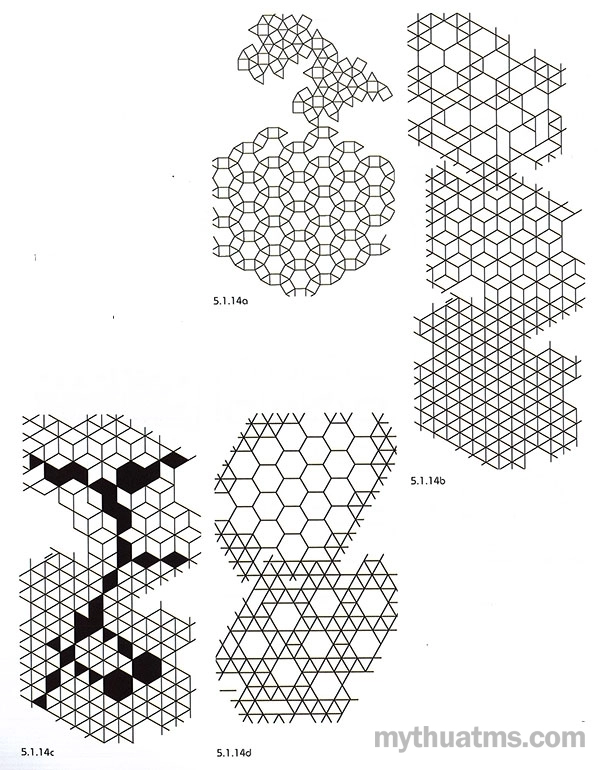
Hình 5.1.14: Tổ chức hệ lưới
a. Hợp nhóm hệ lưới đa lặp: vuông – tam giác đều và vuông – lục giác – tam giác.
b. Hệ lưới tam giác đều biến thể thành hệ tứ giác và hệ đa lặp tam giác – lục giác.
c. Hệ lưới tam giác kết hợp hệ tứ giác. Một phần các ô lưới được tô đen tạo thành hợp nhóm các hình thể kiểu hệ tuyến tính và phân nhánh kiểu tán xạ.
d. Hệ tam giác đều được khoét rỗng tạo nên hệ lưới và ô rỗng lục giác bên trong.
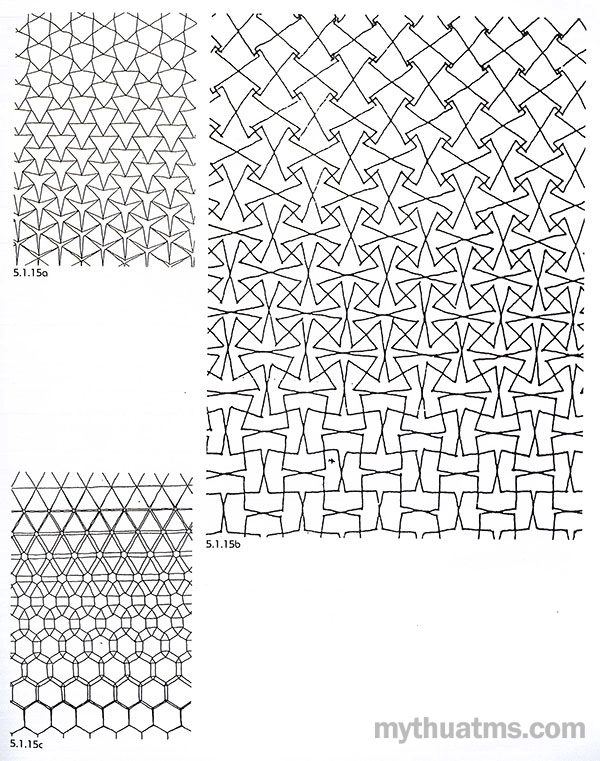
Hình 5.1.15: Biến thể hệ lưới theo cách biến đổi dần hình dạng ô cơ sở
a. Ô lưới lục giác biến đổi dần thành tam giác, thành hình sao ba cạnh.
b. Hình cơ sở kiểu cài lồng biến đổi dần từ hình chữ nhật thành hình lá ba nhánh, thành tứ giác gần vuông.
c. Thay đổi dần dần kích cỡ các hình đơn vị, hình chữ nhật, hình lục giác, tam giác.
* Bài thực hành 5.1.2: Tạo dựng hệ lưới ba chiều
Tạo dựng một hệ lưới ba chiều trên cơ sở ô không gian cơ sở là khối đa diện đều và bán đều, hay khối hộp chữ nhật. Dùng các thủ pháp khoét rỗng khối, chia cắt khối hay tạo các yếu tố diện, tuyến, khối và biến đổi chúng nội tiếp trong hệ lưới ba chiều này. Xem các ví dụ hình 5.1.16.

Hình 5.1.16: Biến đổi mạng 3 chiều (a-c)
a. Hệ mạng được hình thành từ hình lập phương và trụ tròn, kiểu hệ lưới đa lặp, cài lồng (Bài tập sinh viên).
b. Hệ mạng được hình thành từ sự liên kết của khối rỗng đa diện bán đều (khối 3.6.6) thông qua tiếp xúc ở bề mặt tam giác đều. Hình thức nội tiếp, khối trong khối (Bài tập sinh viên).
c. Kiểu mạng lập phương trực giao có biến thể nội tại là các tuyến chéo bên trong (Bài tập sinh viên).

Hình 5.1.16 (d-e)
d. Hệ tuyến mạng đa lặp, sự kết hợp khối đa diện bán đều (3.4.3.4) với khối kim tự tháp, khối lập phương (Bài tập sinh viên).
e. Hợp nhóm các ô lưới trên cơ sở khối lăng trụ tam giác, liên kết kiểu diện tiếp xúc với diện (Bài tập sinh viên).

Hình 5.1.16 (f-g)
f. Mạng kiểu khối hộp chữ nhật, mỗi ô hộp chữ nhật được xử lý nội tại, như thêm diện, thêm khối chóp tam giác (Bài tập sinh viên).
g. Hệ cấu trúc mạng ba chiều trên cơ sở liên kết các khối đa diện đều 4 mặt tam giác (khối 3.3.3.) (Bài tập sinh viên).
- Cấu trúc tự nhiên: Thế giới tự nhiên với vô vàng thể trạng và hệ cấu trúc kỳ thú, con người nghiên cứu và ứng dụng nó vào tạo hình và xây dựng. Có thể phân ra ba cách thức nghiên cứu ứng dụng hệ cấu trúc của tự nhiên cho việc tạo hình thể: a. Mô phỏng, cách điệu hình dạng, hình thể của thế giới tự nhiên; b. Sơ đồ hóa hệ cấu trúc tự nhiên theo khía cạnh cơ cấu, cấu tạo rồi ứng dụng các sơ đồ này dưới nhiều dạng khác nhau; c. Ứng dụng hệ thống tỷ lệ (trên cơ sở nghiên cứu thế giới tự nhiên) để tạo ra sự cân xứng cho một vật thể hoặc nhóm các vật thể dưới ba dạng: hình học, đại số và điều hòa.
Hệ hình học dựa trên các phép dựng, phép chia hình học, lấy các hình cơ bản (hình vuông, hình chữ nhật, hình tam giác, hình tròn…) làm cơ sở.
Hệ đại số dựa vào hướng tiếp cận các hình theo kinh nghiệm theo mẫu hình (đo đạc các hình thể mẫu).
Hệ điều hòa được xây dựng từ quy luật toán học trừu tượng (ví dụ: con số vàng, tỷ lệ vàng, chuỗi số cộng Fibonacci…).
Các hình minh họa dưới đây là ví dụ việc áp dụng hình dạng, cấu trúc của thế giới tự nhiên trong nghệ thuật tạo hình. Xem hình 5.1.17.

Hình 5.1.17: Tạo hình và cấu trúc tự nhiên
a. Hợp nhóm các hình chữ nhật có thiết diện vàng theo cách dùng tuyến điều hòa và chuỗi số cộng Fibonacci.
b. Henry Moore. Per Bogenscutze, German (1966). Một dạng cách điệu hình ảnh thế giới hữu cơ. Các khối có dạng như ống xương sắp đặt liền kề, tiếp xúc nhau phỏng hình dạng và cơ cấu của thân cây.

Hình 5.1.17c: Alexandre Calder. Bản thép cong và ngang có cơ cấu, cấu trúc như hình dáng, khung xương thú bốn chân. Một cách sơ đồ hóa cấu trúc.
Hình 5.1.17d: The Serpentine Gallery Pavillion in London, 2002. Toyo Ito. Cấu trúc kiểu mạng được ứng dụng làm mái và tường trong kiến trúc.

Hình 5.1.17e: The World Trade Center Transportation Hub, New York, 2015. Santiago Calatrava. Cấu trúc kiểu khung xương động vật. Các tuyến hình đơn vị được hợp nhóm theo kiểu biến đổi dần. Một dạng cách điệu và sơ đồ hóa hệ cấu trúc.
Hình 5.1.17f: Quatar National Convention Center in Doha, 2011. Arata Isozaki. Một công trình có hình dáng bên ngoài cấu tạo mô phỏng hình dạng và cơ cấu hữu cơ của thân cây.

Hình 5.1.17g: Taiwan Solar Powered Stadium, 2013, Toyo Ito. Một sân vận động có hình dáng tổng thể như con rắn. Vành mái uyển chuyển với cấu trúc dạng hữu cơ. Kết cấu là hệ thanh kim loại tổ chức dạng mạng, kích cỡ biến chuyển dần.
Hình 5.1.17h: Dongdaemun Design Plaza, Seoul, 2010. Zaha Hadid. Một công trình sáng tác theo cách mô phỏng khối hình hữu cơ. Nó có dáng vẻ một sinh vật nhuyễn thể.
>>> Những yếu tố cơ bản của hình thể (Phần 1)
>>> Hình thể không gian trong thiết kế tạo hình
>>> Màu sắc và hình thể trong tranh sơn dầu (75-95)