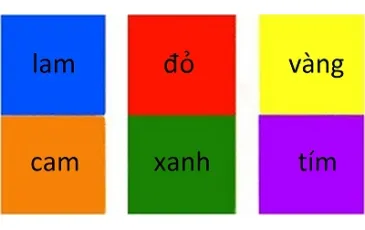
Đối xứng trong nghệ thuật (Phần cuối)
* Mọi con đường đều dẫn tới Lisbon:
Người ta thường hay nói: “Mọi con đường đều dẫn tới Roma”. Nhưng nếu đó là những con đường lát gạch trang trí tuần hoàn, thì chúng sẽ đều dẫn tới Lisbon!
Thành phố Lisbon xinh đẹp nằm bên bờ biển Đại Tây Dương có nhiều khu đi bộ được lát bằng gạch đá vôi (limestone) nhỏ màu trắng và đen, theo một phương pháp truyền thống gọi là “lát gạch Portugal” (Portuguese pavements), tạo thành những ảnh trang trí rất nghệ thuật.

Quảng trường Rossio ở Lisbon với nền ảnh sóng tuần hoàn
Người bạn đồng nghiệp Rui Loja Fernandes của tôi, cựu chủ tịch Hội toán học Portugal và cựu giáo sư tại Đại học Bách khoa Lisbon (Instituto Superior Técnico de Lisboa) có kể rằng, sau khi nghe nói về các nhóm đối xứng trong việc lát gạch, đích thân ông thị trưởng thành phố đã mời các nhà toán học của trường làm cố vấn để đảm bảo rằng tất cả các kiểu nhóm lát gạch khác nhau đều xuất hiện trên các khu đi bộ của Lisbon.
Khi trang trí một mặt phẳng, như là quảng trường Rossio (Ảnh 15) hay là tường nhà, sàn nhà, tấm vải, tấm thảm, v.v. người ta có thể chọn cách trang trí tuần hoàn hai chiều (tức là có hai hướng các viên gạch tam giác, tứ giác hay lục giác đều, nhưng không thể lát mặt phẳng chỉ bằng ngũ giác đều tịnh tiến khác nhau bảo toàn ảnh). Những kiểu trang trí như vậy được gọi là lát gạch (tiếng Anh là tessellation, tiếng Pháp là pavage) tuần hoàn. Bởi ta ảnh đúng là có thể lấy những viên gạch trông giống nhau (hoặc vài kiểu gạch) rồi xếp chúng lại cạnh nhau là sẽ được ảnh trang trí như ý muốn.

Ảnh quảng trường Restauradores ở Lisbon của Jee Wee, với nền được lát đá theo nhóm đối xứng p4.
Tương tự như là các đường viền, các trang trí kiểu lát gạch tuần hoàn cũng có các nhóm đối xứng, mà chúng ta sẽ gọi là nhóm lát gạch theo tiếng Pháp (groupe de pavage, còn tiếng Anh gọi là wallpaper group, tức là nhóm của giấy dán tường). Ngoài các đối xứng tịnh tiến, còn có thể có các đối xứng quay, đối xứng gương và đối xứng lượn. Ví dụ như nền quảng trường Rossio trên Ảnh 15 có đối xứng quay theo góc π (180 độ), còn nền đá hoa trên Ảnh 16 và Ảnh 19 có đối xứng quay theo góc π/2 (90 độ).
Nếu như một kiểu lát gạch tuần hoàn có đối xứng quay, thì vì tính chất tuần hoàn nên góc quay nhỏ nhất phải là một trong các số π,2π/3,π/2,π/6 (ứng với chuyện có thể lát kín mặt phẳng bằng các viên gạch tam giác, tứ giác hay lục giác đều, nhưng không thể lát mặt phẳng chỉ bằng ngũ giác đều chẳng hạn). Khi có cả đối xứng quay lẫn đối xứng gương, người ta có thể xét xem trục của đối xứng gương có chứa tâm của đối xứng quay hay không. Ví dụ trên Ảnh 15 có tâm của phép quay nằm ngoài trục đối xứng (xem Ảnh 17), còn ví dụ trên Ảnh 19 có tâm của phép quay nằm trên trục đối xứng.

Đường đỏ là trục đối xứng gương, điểm xanh là tâm của đối xứng xoay 180 độ. Nguồn: kleinproject.org
Tương tự như là đối với các nhóm đường viền, ta có thể phân loại các nhóm lát gạch theo chuyện nó có đối xứng quay hay không và góc quay là bao nhiêu nếu có, rồi nó có đối xứng gương hay không, có đối xứng lượn hay không, và tâm của đối xứng quay có nằm trên trục đối xứng gương hay không.
Người đầu tiên đưa ra phân loại đầy đủ cho các nhóm này là nhà toán học và khoáng vật học người Nga Evgraf Fedorov (1853–1919) vào cuối thế kỷ 19. Có tổng cộng 17 nhóm lát gạch khác nhau, ứng với 17 kiểu lát gạch tuần hoàn khác nhau. Ảnh 18 là sơ đồ minh họa toàn bộ 17 kiểu đó.
Mỗi một ảnh con trên Ảnh 18 ứng với một kiểu lát gạch. Miền tô xanh là miền mà nếu làm viên gạch có ảnh như vậy, rồi dịch chuyển nó theo các phép biến đổi đối xứng trong nhóm tương ứng, thì ta lát kín vừa khít được toàn bộ mặt phẳng.
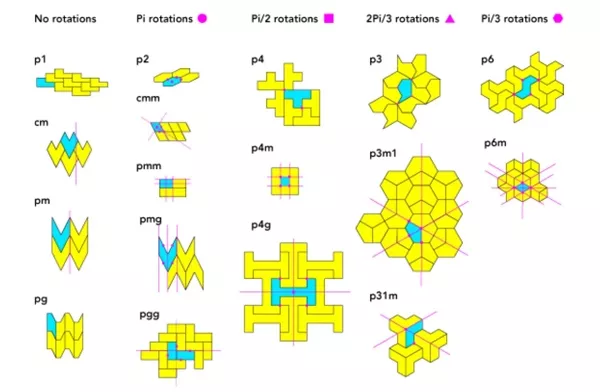
Sơ đồ của 17 nhóm lát gạch
Trong số các ký hiệu của 17 kiểu nhóm đối xứng trên ảnh 18, có 2 ký hiệu bắt đầu bằng chữ cái c, có nghĩa là “centred” (ở giữa). Mỗi kiểu “c” đó đều có hai vector tịnh tiến có độ dài bằng nhau (tạo thành ảnh thoi), nhưng trục đối xứng hoặc trục glide của ảnh không song song với một trong hai vector đó mà lại “nằm giữa” hai vector (tức là song song với tổng của chúng). Tất cả các kiểu còn lại đều bắt đầu bằng chữ cái p, có nghĩa là "primitive" (nguyên thủy): ở các kiểu này, các trục đối xứng hay glide song song với các vector tịnh tiến "nguyên thủy" của ảnh.

Quảng trường Camoes ở Lisbon lát gạch theo nhóm p4m.
Chữ số trong ký hiệu các kiểu cho biết nó có phép quay theo góc bao nhiêu: nếu chữ số là k thì góc quay nhỏ nhất là 2π/k. Ví dụ nếu có chữ số 4 thì có phép quay theo góc π/2 = 2π/4. Chữ cái m trong ký hiệu dùng để chỉ đối xứng gương (mirror), còn chữ cái g dùng để chỉ đối xứng lượn (glide).
Danh sách chi tiết 17 kiểu như sau:
Kiểu thứ nhất, ký hiệu là p1, là kiểu chỉ có các đối xứng tịnh tiến, ngoài ra không còn thêm đối xứng nào khác. Ảnh 20 phía bên trái là một ví dụ.
Kiểu thứ hai, ký hiệu là pg, có thêm glide, nhưng không có đối xứng quay hay đối xứng gương. Trong kiểu này có hai hướng tịnh tiến vuông góc với nhau. Tranh lát gạch "Kỵ sĩ" của Maurits Cornelis Escher trên Ảnh 21 là một ví dụ tiêu biểu (nếu ta bỏ qua màu của các con ngựa): phép glide chuyển con ngựa màu nhạt thành con ngựa màu thẫm.

Một trang trí giấy dán tường có nhóm đối xứng p1, và một trang trí kiểu Ai Cập có nhóm đối xứng pm.
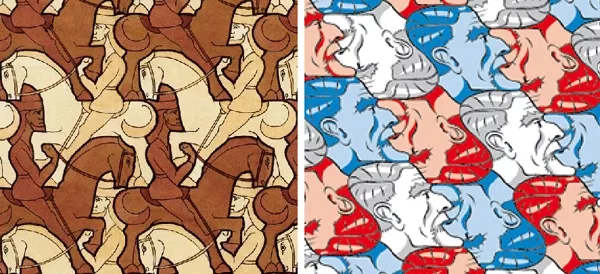
Tranh lát gạch "kỵ sĩ" và "đầu Escher" của Escher.
Kiểu thứ ba, ký hiệu là cm, không có đối xứng quay nhưng có đối xứng gương, và có thêm glide với trục của glide khác với trục đối xứng gương. Vải hoa lys (hoa loa kèn) trên Ảnh 3.22 bên trái là một ví dụ: Các trục đối xứng gương ở đây chính là các trục đối xứng của các bông hoa ly, còn mỗi trục glide thì song song và nằm giữa hai trục đối xứng gương liên tiếp.

Vải trang trí hoa ly có nhóm đối xứng kiểu cm và tấm thảm phương Đông có nhóm đối xứng kiểu pmm.
Kiểu thứ tư, ký hiệu là pm, không có đối xứng quay nhưng có đối xứng gương, và không có glide với trục nằm ngoài trục đối xứng gương như kiểu thứ ba. Một ví dụ là trang trí kiểu Ai Cập trên ảnh 20 phía bên phải. Chú ý rằng kiểu này có một vector tịnh tiến song song với các trục đối xứng và một vector tịnh tiến vuông góc với các trục đối xứng.
Kiểu thứ năm, ký hiệu là p2, ngoài các đối xứng tịnh tiến còn có thêm đối xứng quay theo góc π, và ngoài ra không có thêm đối xứng nào khác. Ảnh lát gạch đầu ông Escher (với những đầu chổng ngược qua phép quay 180 độ) trên ảnh 21 là một ví dụ.
Kiểu thứ sáu, ký hiệu là pgg, không có đối xứng gương, nhưng có hai họ đối xứng glide với các trục glide vuông góc với nhau. Kiểu này cũng có đối xứng quay 180 độ, vì nếu lấy tích của hai glide với các trục vuông góc với nhau thì được một phép quay như vậy. Ảnh lát sàn gỗ 23 là một ví dụ (nếu ta coi tất cả các viên gỗ ảnh chữ nhật là giống hệt nhau). Kiểu lát này còn được gọi là kiểu "xương cá trích" (herringbone).

Sát lát gỗ có nhóm đối xứng kiểu pgg, còn ảnh trang trí trên bình cổ từ Kerma (Sudan) đối xứng kiểu pmg.
Kiểu thứ bảy, ký hiệu là pmg, vừa có đối xứng gương, vừa có đối xứng quay 180 độ với tâm không nằm trên đối xứng gương. Tích của hai phép đối xứng đó là phép glide, nên trong ký hiệu của kiểu này có cả m (mirror) và g (glide). Chiếc bình cổ đại trên ảnh 23 có kiểu trang trí này trên thành bình.
Kiểu thứ tám, ký hiệu là pmm. Thay vì có đối xứng gương theo một hướng và đối xứng glide theo hướng vuông góc với nó, kiểu pmm có hai đối xứng gương theo hai hướng vuông góc với nhau, và tích của chúng cũng là một phép quay 180 độ. Tấm thảm ở bên phải ảnh 22 là một ví dụ.

Mặt tường gạch có nhóm đối xứng kiểu cmm.
Kiểu thứ chín, ký hiệu là cmm có các đối xứng giống như là kiểu pmm, nhưng ngoài ra còn có các phép quay 180 độ với tâm không nằm trên các trục của các đối xứng gương. Ảnh xây gạch thành tường như trên ảnh 24 là một ví dụ về nhóm lát gạch kiểu cmm. Các điểm tô đỏ và tô xanh trên ảnh đều là tâm của các đối xứng quay 180 độ của ảnh. Các trục đối xứng gương chỉ đi qua các điểm đỏ chứ không đi qua các điểm xanh.

Một mảnh tường ở Alhambra lát gạch theo nhóm p3.
Kiểu thứ mười, ký hiệu là p3, có đối xứng quay với góc nhỏ nhất là 1/3 vòng tròn và không có đối xứng gương. Ảnh 25 là một ví dụ.
Kiểu thứ mười một, ký hiệu là p3m1, có đối xứng quay với góc 1/3 vòng tròn, có đối xứng gương, và tâm của đối xứng quay nằm trên trục đối xứng gương.

Một cửa sổ tại lăng Salim Chishti, Ấn Độ, có nhiều kiểu nhóm đối xứng lát gạch.
Kiểu thứ mười hai, ký hiệu là p31m, có đối xứng gương, có đối xứng quay với góc 1/4 vòng tròn và tâm của nó không nằm trên trục của đối xứng quay.
Kiểu thứ mười ba, ký hiệu là p4, có đối xứng quay với góc 1/4 vòng tròn (tức là π/2) và không có đối xứng gương. Ảnh 16 là một ví dụ.
Kiểu thứ mười bốn, ký hiệu là p4g, có đối xứng quay với góc 1/4 vòng tròn, có đối xứng gương, và có đối xứng glide với trục tạo thành góc 45 độ với trục của đối xứng gương.
Kiểu thứ mười lăm, ký hiệu là p4m, có đối xứng quay với góc 1/4 vòng tròn, và có hai đối xứng gương với các trục tạo với nhau một góc 45 độ. Ảnh 19 là một ví dụ.
Kiểu thứ mười sáu, ký hiệu là p6, có đối xứng quay với góc 1/6 vòng tròn (tức là π/3) và không có có đối xứng gương. Ảnh 27 bên phải là một ví dụ.

Sàn đá hoa ở Duomo di Siena (Toscana, Italia) có nhóm đối xứng p6m, còn tranh "Con bướm" của Escher có nhóm đối xứng p6..
Kiểu thứ mười bảy, ký hiệu là p6m, có góc quay 1/6 vòng tròn và có đối xứng gương. Ảnh 27 bên trái là một ví dụ.
Ngoài Lisbon, có một nơi khác cũng được coi là có đủ 17 kiểu nhóm lát gạch là khu cung điện Alhambra (tiếng Ả Rập có nghĩa là "Đỏ") do những người Hồi Giáo xây ở Granada, Tây Ban Nha, từ thế kỷ 13. Đây là một cung điện nguy ra, với rất nhiều trang trí tuần hoàn (và cả không tuần hoàn) đẹp trên tường. Tuy nhiên, chưa thấy ai công bố kiểm chứng là nó có đủ 17 kiểu lát gạch

Trần gian phòng Abencerrajes tại cung điện Alhambra, với nhiều trang trí kiểu lát gạch khác nhau trên tường.
Người ta nói rằng họa sĩ Escher khi đi thăm Alhambra đã có được ý tưởng và cảm hứng vẽ các tranh lát gạch nổi tiếng của ông từ các ảnh trang trí trên tường của cung điện này, và tranh của Escher có chứa đủ 17 kiểu nhóm lát gạch. Trong sách “Các bài giảng về toán cho Mirella” cũng có một chương về tạo ảnh trang trí bắt chước Escher bằng cách sử dụng các phép đối xứng.
Vào thập kỷ 1980, nhà toán học William Thurston nghĩ ra một phương pháp ảnh học mới, dựa trên lý thuyết về orbifold (có thể hiểu orbifold như là tập hợp các quỹ đạo (orbit) của một nhóm hữu hạn tác động lên một đa tạp), để phân loại các nhóm lát gạch. Phương pháp của Thurston cho ra giải thích gọn ghẽ vì sao chỉ có 17 nhóm, nhưng để mô tả tác động của các nhóm đó trên mặt phẳng thì vẫn phải làm như trên.

Hai ví dụ lát gạch 3 chiều của Andrew Kepert từ wikimedia.
Các viên gạch ở đây là “truncated octahedra” (“bát diện cụt”) hoặc “rhombic dodecahdra” (“thập nhị diện con thoi”).
Nếu như trên mặt phẳng “chỉ có” 17 cách lát gạch tuần hoàn, thì trong không gian ba chiều số nhóm “lát không gian” Người ta nói rằng họa sĩ Escher khi đi thăm Alhambra đã có được ý tưởng và cảm hứng vẽ các tranh lát gạch nổi tiếng của ông từ các ảnh trang trí trên tường của cung điện này,
* Đối xứng trên không gian phi Euclid:
Ngoài mặt phẳng ra, còn có hai loại mặt khác mà trên đó cũng có các phép tịnh tiến, phép phản chiếu và phép quay bảo toàn khoảng cách, là mặt cầu và mặt hyperbolic (hay còn gọi là mặt Lobachevsky). Chúng là những không gian phi Euclid. Các không gian phi Euclid này cũng có thể được lát gạch tương tự như là mặt phẳng, và những ảnh lát gạch đó cũng có thể cho ra những tác phẩm đẹp mắt.

Một quả cầu trang trí "Thiên thần và quỷ sứ" dựa theo tranh Escher có bán trên amazon,
và hai mô ảnh lát gạch ảnh cầu bằng giấy và đất sét của Makoto Nakamura.
Ảnh 30 là những ví dụ về lát gạch trên ảnh cầu. Vấn đề lát gạch phủ ảnh cầu liên quan đến vấn đề phân loại các đa diện đều và gần đều.
Có thể ảnh dung mặt hyperbolic dưới dạng một cái đĩa (không có biên), gọi là đĩa Poincaré. Khoảng cách trên đĩa đó không giống khoảng cách trên mặt phẳng bình thường, mà tăng lên rất nhanh khi các điểm tiến tới gần biên của đĩa.

Lát mặt hyperbolic bằng ảnh hoa hồng
Ảnh 31 là ví dụ về lát mặt hyperbolic bằng ảnh hoa hồng đã cắt mép thành lục giác (cho hoa hồng trắng) hoặc tứ giác (cho hoa hồng đỏ) hyperbolic, sử dụng phần mềm toán học của Malin Christersson. Chú ý là, tuy các hoa hồng càng gần mép đường tròn thì trông càng bé tí xíu, nhưng đối với khoảng cách hyperbolic thì tất cả các bông hoa hồng trên cùng một ảnh đều to bằng nhau.
* Lát gạch không tuần hoàn:
Vào năm 1982, nhà vật lý Dan Shechtman phát hiện ra sự tồn tại của những vật rắn mà cấu trúc phân tử của nó không tuần hoàn. Người ta gọi những cấu trúc này là giả tinh thể (quasicrystal). Nhờ phát hiện đó mà ông đã được giải Nobel vào năm 2011.
Về mặt toán học, cấu trúc giả tinh thể có thể được hiểu như là việc lát phủ kín không gian bằng một vài loại viên gạch, một cách không tuần hoàn. Các kiểu lát gạch không tuần hoàn và các cấu trúc giả tinh thể vẫn đang là một đề tài nghiên cứu khoa học quan trọng ngày nay.
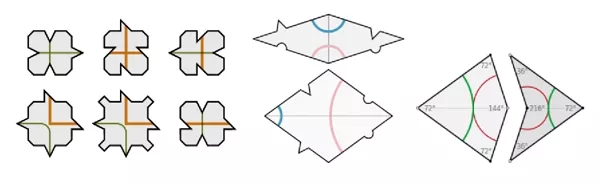
Bộ 6 kiểu viên gạch của Raphael Robinson, và hai bộ gạch của Penrose mỗi bộ 2 viên
Người ta đã xây dựng các lý thuyết về các kiểu gạch có tính chất ép cho việc lát gạch không thể tuần hoàn. Raphael Robinson có lẽ là người đầu tiên chứng minh được, vào năm 1971, về sự tồn tại của những kiểu viên gạch lát kín được mặt phẳng sao cho không thể lát chúng một cách tuần hoàn. Ông nghĩ ra một bộ 6 ảnh viên gạch như trên ảnh 32 bên trái. Dùng các viên gạch như thế có thể lát kín mặt phẳng, như là minh họa trên ảnh 33. Chỉ có điều, mỗi ảnh vuông màu da cam do gạch lát tạo nên đều bắt buộc nằm ở góc của một ảnh vuông màu da cam to hơn. Từ đó suy ra là ảnh lát gạch không thể tuần hoàn.

Lát mặt phẳng bằng các viên gạch của Robinson.
Bộ viên gạch lát không thể tuần hoàn đơn giản và nổi tiếng nhất có lẽ thuộc về nhà toán học và vật lý Roger Penrose (sinh năm 1931). Một bộ gạch của Penrose chỉ gồm có 2 ảnh viên gạch, đều là ảnh thoi, như trên ảnh 32 ở giữa. Các góc của các ảnh thoi đó lần lượt là π/5,4π/5,2π/5 và 3π/5 (tương tự như là các góc của ngũ giác đều và của ảnh sao 5 cánh đều), và bởi vậy chúng có thể cộng với nhau thành 2π để lát khớp tại các đỉnh. Một bộ gạch 2 viên khác của Penrose, với một viên ảnh cánh diều và một viên ảnh mũi tên, như trên ảnh 32 bên phải, cũng có các tính chất tương tự. Các viên gạch kiểu Penrose có được sản xuất và dùng để lát sàn nhà ở nhiều nơi trên thế giới.

Tranh sơn dầu của họa sĩ Urs Schmid (1995) vẽ một kiểu lát gạch Penrose dùng các viên gạch ảnh thoi.
Penrose không phải là người đầu tiên nghĩ ra các viên gạch có góc là bội số của π/5. Ông lấy ý tưởng đó từ các tác phẩm của Albrecht Durer và Johannes Kepler từ thời thế kỷ 16-17.¨ Từ trước đó nữa, các nghệ sĩ Hồi Giáo (ắt hẳn đồng thời cũng là những nhà toán học) đã nghĩ ra việc dùng các "viên gạch" như trên ảnh 35, gọi là girih, có các góc là bội của π/5, để lát trang trí. Viên girih to nhất có ảnh 10-giác đều. Tiếp đến là viên ảnh lục giác với các góc nhọn bằng 2π/5 và các góc tù bằng 4π/5. Tiếp đó là ảnh cái nơ con bướm với các góc nhọn cũng bằng 2π/5, rồi ảnh thoi với các góc nhọn cũng bằng 2π/5, và sau cùng là ảnh ngũ giác đều. Girih theo tiếng Persia có nghĩa là "đường nút", để chỉ các đường trang trí gấp khúc được vẽ trên các viên gạch.
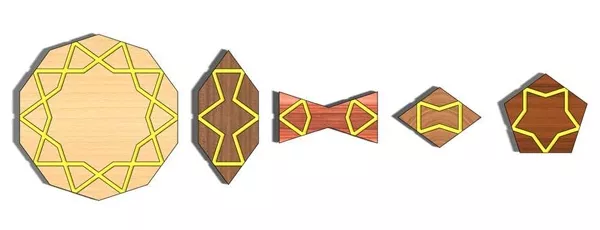
Các viên girih.
Các viên gạch trên ảnh 35 xuất hiện từ quãng cuối thế kỷ 12 ở Thổ Nhĩ Kỳ, với công dụng là giúp các nghệ nhân trong việc thiết kế ảnh trang trí, còn bản thân kiểu trang trí girih của Hồi Giáo đã có từ trước đó. Sau khi có bản thiết kế thì các nghệ nhân không cần phải làm ra các viên gạch như trên
Ảnh 35, mà cốt làm sao xây được tường với hoa văn girih giống trong bản thiết kế. Trên các bức tường trang trí girih, nói chung sẽ không nhìn thấy biên của các "viên gạch girih" như trên, bởi vì thực ra không có các viên gạch đó.

Bìa một quyển kinh Quoran từ thế kỷ 14, và thiết kế girih của nó.
Nguồn: David James, Qur’ans of the Mamluks (Thames & Hudson) & aramcowworld.com.
Với kiểu thiết kế girih, người Hồi Giáo đã không chỉ tạo được những ảnh nghệ thuật lát tường tuần hoàn, mà cả những ảnh không tuần hoàn nhưng có đối xứng khác, ví dụ như là đối xứng kiểu sao 5 cánh hay 10 cánh (đối xứng quay theo góc π/5; không thể tuần hoàn nếu có đối xứng quay này), như trên ảnh 36 và ảnh 37. Hơn nữa, các "viên gạch" girih chỉ có tính chất trợ giúp cho thiết kế cho dễ thôi, chứ một ảnh trang trí girih không nhất thiết phải xếp được từ đúng các "viên gạch girih" đó, mà có những chỗ có thể lệch đi, dùng những góc khác, "gạch" khác.

Khu lăng tẩm "Shah-i Zinda" ("Vua Sống") ở Samarquand, Uzbekistan
(ảnh của Fulvio Spada), và một trang trí girih bên trong.
>>> Đối xứng trong nghệ thuật (Phần 1)
>>> Nguyên lý hàng lối, cân đối, tự do trong cơ sở tạo hình