Hội họa toán học của M.C.Escher

M.C.Escher (1898-1972). Tự họa

Escher tự gọi mình là “họa sĩ đồ họa”, ông chuyên về nghệ thuật khắc gỗ và in thạch bản. Tên đầy đủ của ông là Maurits Cornelis Escher, sinh năm 1898 tại Leeuwarden, Hà Lan. Gia đình định cho ông theo nghề kiến trúc của cha, nhưng do bị điểm kém ở trường và lại có thiên hướng vẽ và thiết kế, cuối cùng ông theo con đường đồ họa. Ông sống suốt đời tại châu Âu và mất ở Hilversum, Hà Lan vào năm 1972.

Mãi đến thập niên 50 của thế kỷ 20, tác phẩm của ông hầu như vẫn chưa được biết tới, nhưng vào năm 1956 ông có cuộc triển lãm quan trọng đầu tiên, người ta viết về ông trên tạp chí Time và ông trở nên nổi tiếng khắp thế giới. Trong số những người hâm mộ ông có những nhà toán học, bởi họ nhận thấy trong tác phẩm của ông một sự hình tượng hóa phi thường các nguyên lý và ý tưởng toán học.

Điều này càng phi thường bời nhà họa sĩ Hà Lan này không hề được đào tạo chính quy về toán; kiến thức toán học của ông chỉ dừng ở cấp trung học. Càng sáng tác, ông càng lấy cảm hứng từ những ý tưởng toán học mà ông đọc được trong khi trực tiếp làm các cấu trúc trong mặt phẳng và hình học xạ ảnh, để rồi cuối cùng nắm bắt được thực chất của các hình học phi Ơclít như ta sẽ thấy dưới đây. Ông cũng say mê những nghịch lý và hình thể “bất khả” (không thể có được) và sử dụng một ý tưởng của Roger Penrose để phát triển nhiều tác phẩm xuất sắc. Sáng tạo của Escher bao hàm các lĩnh vực: hình thể của không gian, lôgic của không gian và tự qui chiếu và thông tin.

Hình thể của không gian

Trong những tác phẩm quan trọng nhất của Escher xét từ góc độ toán học, có những tác phẩm đề cập đến thực chất của bản thân không gian.

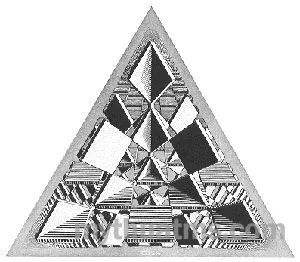
Ba mặt phẳng giao nhau (1954)

Bức khảm “Ba mặt phẳng giao nhau” là một điểm bắt đầu thích hợp để điểm qua các tác phẩm này, bởi nó tiêu biểu cho mối quan tâm của họa sĩ về các chiều của không gian, cũng như cho khả năng của trí tuệ trong việc nhận thức không gian ba chiều trong một biễu diễn hai chiều. Như ta sẽ thấy trong phần kế, Escher thường khai thác tính chất sau để đạt những hiệu quả thị giác lạ. Lấy cảm hứng từ một bức vẽ trong cuốn sách của nhà toán học H.S.M Coxeter, Escher tạo ra nhiều hình tượng đẹp về không gian hyperbol như trong bức khắc gỗ “Giới hạn vòng tròn III” (Circle Limit III). Đây là một trong hai loại không gian phi Ơclít, vàmô hình đưa ra trong tác phẩm của Escher thực sự là nhờ có nhà toán học Pháp Poincaré. Để có ý niệm về cái không gian này, hãy hình dung bạn đang ở trong chính bức tường tranh.

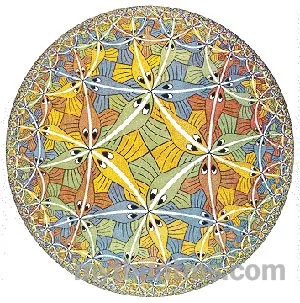
Giới hạn vòng tròn III (1958)

Khi đi từ trung tâm tranh về phía rìa tranh, bạn sẽ từ từ rút ngắn lại hệt như những con cá trong tranh, thế nên để có thể thực sự đi đến rìa tranh, bạn phải đi qua một quãng đường mà đối với bạn là dài vô tận. Thật ra đối với bạn, khi đang ở bên trong không gian hyperbol này, bạn sẽ không nhận ra ngay có gì bất thường, bởi xét cho cùng bạn cũng phải vượt qua một khoảng cách vô tận mới tới được rìa của không gian Ơclít thông thường. Tuy nhiên, nếu quan sát cẩn thận, có thể bạn sẽ bắt đầu nhận ra vài thứ kỳ lạ, chẳng hạn như tất cả các hình tam giác tương tự đều cùng một cỡ, và không một hình phẳng nào bạn vẽ sẽ có bốn góc đúng – nghĩa là, không gian này không có hình vuông hay hình chữ nhật. Kỳ là quá đi chứ! Còn khác thường hơn nữa là cái không gian trong bức khắc gỗ “Những con rắn”. Ở đây, không gian tiến về vô cực theo cả hai chiều, cả về phía rìa lẫn về phía trung tâm vòng tròn, như ta có thể suy ra từ những đường tròn cài vào nhau và không ngừng co rút lại. Nếu bạn sống trong cái không gian này thì sẽ như thế nào?

Những con rắn

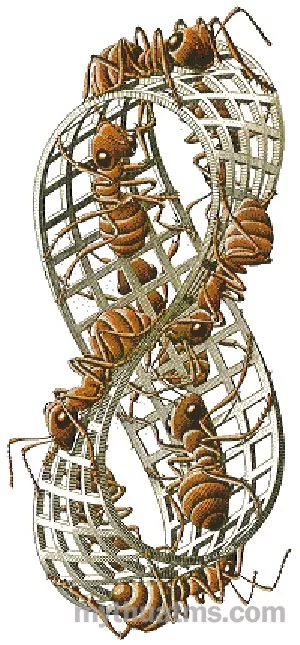
Hình ảnh con kiến và Dải Môbius II (1963)

Một bức tranh in đá khác rất nổi tiếng, gọi là “Phòng triển lãm ảnh” (Print Gallery) sử dụng cả lôgic lẫn hình học tôpo của không gian. Ở đây, một thanh niên trong phòng trưng bày mỹ thuật đang nhìn bức ảnh một thành phố ven biển với một cửa hàng dọc theo các ụ tàu, còn trong cửa hàng đó là một phòng trưng bày mỹ thuật, với một thanh niên đang nhìn bức ảnh một thành phố ven biển... nhưng đợi đã! Điều gì xảy ra vậy?

Phòng triển lãm (1956)

Mọi tác phẩm của Escher đều đáng cho ta ngắm kỹ, nhưng bức này càng đáng ngắm kỹ hơn. Bằng cách nào đó, Escher đã cuộn không gian vào trong chính nó, để cho chàng thành niên vừa ở trong tranh vừa ở ngoài tranh cùng một lúc. Bí mật của việc này được vén lên phần nào nếu ta xem những phác thảo của họa sĩ trong quá trình làm việc. Chú ý rằng tỉ lệ những đường kẻ tăng lên liên tục theo chiều kim đồng hồ. Và hãy chú ý đặc biệt đến cái lỗ ở tâm điểm. Một nhà toán học sẽ gọi đây là một điểm kỳ dị (singularity), nơi mà cơ cấu của không gian không còn giữ được nguyên vẹn. Chẳng có cách nào dệt cái không gian kỳ quái này thành một toàn thể liền mạch, nhưng Escher, thay vì cố che đậy điều đó bằng cách này cách nọ, đã ghi đậm dấu ấn tên mình vào ngay chính giữa không gian đó.
Lôgic của không gian

Dùng chữ “lôgic” của không gian, chúng tôi muốn nói về những quan hệ không gian giữa các vật thể vật lý, những quan hệ thiết yếu mà nếu bị vi phạm sẽ dẫn đến những nghịch lý thị giác, đôi khi gọi là ảo giác quang học. Mọi họa sĩ đều quan tâm đến lôgic của không gian, và nhiều người đã sử dụng những quy tắc của nó một cách hoàn toàn có dụng ý.

Khối lập phương với những dải duybăng (1957)

Picasso chẳng hạn. Escher hiểu rằng hình học không gian xác định lôgic của không gian, và tương tự, lôgic của không gian xác định hình học của nó. Một trong những đặc tính của lôgic không gian mà ông thường áp dụng là sự biến ảo của ánh sáng và bóng tối trên các vật thể lõm và lồi. Trong bức tranh khắc đá “Khối lập phương với những dải duybăng”, chỗ thắt nút của dải duybăng là chìa khóa thị giác để ta nhận biết chúng quanh quanh khối lập phương theo cách nào. Tuy nhiên, nếu ta tin vào mắt mình thì ta không thể tin vào những dải duybăng!

Một trong những quan tâm chủ chốt của Escher là luật viễn cận. Trong mọi bức vẽ viễn cận, các điểm ảo được lựa chọn nhằm miêu tả cho người xem (các) điểm nằm ở vô cực. Chính việc nghiên cứu luật viễn cận và các ìđiểm ở vô cực” của Alberti, Desargues và những người khác trong thời Phục hưng đã dẫn trực tiếp đến lĩnh vực hình ánh xạ (đúng ra là hình học xạ ảnh, nguyên văn là projective geometry )ngày này.

Cao và Thấp (1947)

Bằng cách đưa ra những điểm ảo khác thường và buộc các yếu tố trong một bố cục phải tuân theo chúng, Escher có thể tạo nên những cảnh mà trong đó hướng “trên/dưới” và “trái/phải” của các yếu tố trong đó hoán vị cho nhau tùy theo hướng nhìn của người xem. Trong tác phẩm “Cao và Thấp”, họa sĩ đặt năm điểm ảo: trên trái và trên phải, dưới trái và dưới phải, chính giữa. Kết quả là trong nửa dưới của bố cục người xem nhìn lên, nhưng trong nửa trên của bố cục, người xem lại nhìn xuống. Để nhấn mạnh thêm điều ông đã đạt được, Escher cho hai nửa trên và nửa dưới mô tả cùng một bố cục.

Một loại “tranh vẽ bất khả” khác dựa vào việc bộ não của chúng ta có đặc tính bất di bất dịch đòi phải có những đầu mối thị giác mới xây dựng được một vật thể ba chiều từ một hình tượng hai chiều. Escher đã tạo ra nhiều tác phẩm về loại này.

Một trong những tác phẩm lý thú nhất dựa trên ý tưởng của nhà toán học Roger Penrose – cái tam giác bất khả (không thể có). Trong bức tranh in đá “Thác nước” này, tác giả kết hợp hai tam giác Penrose thành một hình thể bất khả. Ta thấy ngay lập tức một lý do vì sao lôgic không gian phải loại trừ một cấu trúc như vậy: thác nước là một hệ khép kín, thế mà nó làm quay cối xay liên tục giống như một cái máy vĩnh cửu, do đó vi phạm định luật bảo toàn năng lượng (lưu ý những khối lập phương và khối tám mặt giao nhau trên các ngọn tháp).

Thác nước (1961)

Tự quy chiếu và thông tin

Quan hệ giữa tác phẩm của Escher với các lĩnh vực khoa học thông tin và trí tuệ nhân tạo thường bị xem nhẹ trong nhiều nghiên cứu gần đây, nhưng cuốn sách “Godel, Escher, Bach: An Eternal Golden Braid” của Douglas R. Hofstafter (đoạt giải Pulitzer năm 1980) đã buộc người ta nhìn nhận lại tầm quan trọng của tác phẩm Escher đối với lĩnh vực này.

Những bàn tay vẽ (1948)

Một khái niệm trung tâm mà Escher nắm được, đó là tự quy chiếu (self-reference) mà nhiều người cho là gần ngay điểm mấu chốt sự bí ẩn của ý thức – và khả năng của não trong việc xử lý thông tin một cách hoàn hảo mà chưa một máy tính nào bắt chước nổi. Bức tranh in đá “Những bàn tay vẽ” (Drawing Hands) và tranh khắc gỗ “Cá và Vảy” (Fish anh Scales), mỗi bức nắm bắt ý tưởng bừng một cách khác nhau. Trong bức “Những bàn tay vẽ”, sự tự quy chiếu là trực tiếp và thuộc nhận thức; hai bàn tay tự vẽ chính mình cũng hệt như ý thức tự xem xét và tự dựng nên mình, một cách bí ẩn, trong đó cái ngã và cái ngã tự quy chiếu không tách rời nhau và đồng đẳng với nhau. Mặt khác, trong “Cá và Vây”, sự tự quy chiếu mang tính chức năng nhiều hơn; có lẽ đúng hơn nên gọi là “tự tương đồng” (self-resemblance). Bằng cách này, bức tranh mô tả không chỉ cá mà mọi loài hữu cơ, bởi lẽ mặc dù chúng ta không được tạo thành từ những bản sao nhỏ của chính chúng ta – ít nhất về mặt vật lý, nhưng, theo lý thuyết thông tin, chúng ta được tạo thành chính bằng cách như thế, bởi mỗi tế bào của cơ thể ta đều mang đầy đủ thông tin dưới dạng DNA mô tả toàn bộ sinh vật.

Cá và Vây (1959)

Ở cấp độ sâu hơn, ta có thể gặp tự quy chiếu trong cách những thế giới nhận thức của chúng ta phản ánh và giao thoa với nhau. Mỗi chúng ta giống như một nhân vật trong một cuốn sách đang đọc câu chuyện của chính mình, hoặc như bức tranh một chiếc gương đang phản chiếu khung cảnh của chính nó. Nhiều tác phẩm của Escher đưa ra chủ đề những thế giới giao thoa với nhau này, song ở đây ta chỉ xét một trong nhiều ví dụ. Như thường thấy trong cách tác giả xử lý ý tưởng này, bức “Ba khối cầu II” sử dụng đặc tính phản chiếu của một tấm gương cầu. Ở đây, như Hofstadter nhận xét, ìmỗi bộ phận của thế giới dường như đều chứ đựng và được chứa đựng trong mỗi bộ phận khác...”. Các khối cầu phản chiếu lẫn nhau, phản chiếu họa sĩ, căn phòng nơi ông vẽ, cả tờ giấy trên đó ông vẽ các khối cầu này.

Và như vậy ta kết thúc ở nơi ta bắt đầu, với một bức tự họa: thế giới là phản ánh của họa sĩ, họa sĩ phản ánh trong tác phẩm.

- Trần Tiến Cao Đăng biên dịch -